Các câu hỏi tương tự
Giả sử đồ thị hàm số
y
m
2
+
1
x
4
-
2
m
x
2
+
m
2
+
1
có 3 điểm cực trị là A, B ,C mà
x
A
x
B
x
C
. Khi quay t...
Đọc tiếp
Giả sử đồ thị hàm số y = m 2 + 1 x 4 - 2 m x 2 + m 2 + 1 có 3 điểm cực trị là A, B ,C mà x A < x B < x C . Khi quay tam giác ABC quanh cạnh AC ta được một khối tròn xoay. Giá trị của m để thể tích của khối tròn xoay đó lớn nhất thuộc khoảng nào trong các khoảng dưới đây:
A. (4;6)
B. (2;4)
C. (-2;0)
D. (0;2)
Cho hàm số bậc ba yf(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y|f(x)+m| có ba điểm cực trị là: A.
m
≤
-
1
hoặc
m
≥
3
B.
m
≤
-
3
hoặc
m
≥
1
C. m -1 hoặc m 3 D.
1
≤
m
≤
3
Đọc tiếp
Cho hàm số bậc ba y=f(x) có đồ thị nhu hình vẽ bên. Tất cả các giá trị của tham số m để hàm số y=|f(x)+m| có ba điểm cực trị là:
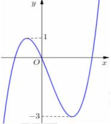
A. m ≤ - 1 hoặc m ≥ 3
B. m ≤ - 3 hoặc m ≥ 1
C. m = -1 hoặc m = 3
D. 1 ≤ m ≤ 3
Cho hàm số
y
x
3
−
3
m
x
+
1
1
.
Cho A(2;3) tìm m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A A. m1/2 B. m-3/2 C. m-1/2 D. m3/2
Đọc tiếp
Cho hàm số y = x 3 − 3 m x + 1 1 . Cho A(2;3) tìm m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A
A. m=1/2
B. m=-3/2
C. m=-1/2
D. m=3/2
Cho hàm số
y
-
x
3
+
3
x
2
+
m
(m là tham số) có đồ thị (C). Gọi A, B là các điểm cực trị của đồ thị (C). Khi đó, số giá trị của tham số m để diện tích tam giác OAB (O là gốc tọa độ) bằng 1 là: A. 0 B. 2 C. 1 D. 3
Đọc tiếp
Cho hàm số y = - x 3 + 3 x 2 + m (m là tham số) có đồ thị (C). Gọi A, B là các điểm cực trị của đồ thị (C). Khi đó, số giá trị của tham số m để diện tích tam giác OAB (O là gốc tọa độ) bằng 1 là:
A. 0
B. 2
C. 1
D. 3
Cho hàm số
y
1
4
x
4
-
3
x
2
có đồ thị (C) . Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M (
x
1
;
y
1
) N (
x
2
;
y
2
) ( M ,N khác A ) thỏa mãn
y
1
-...
Đọc tiếp
Cho hàm số y = 1 4 x 4 - 3 x 2 có đồ thị (C) . Có bao nhiêu điểm A thuộc (C) sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M ( x 1 ; y 1 ) N ( x 2 ; y 2 ) ( M ,N khác A ) thỏa mãn y 1 - y 2 = 5 x 1 - x 2 .
A. 1.
B. 2 .
C. 0 .
D. 3 .
Cho hàm số bậc ba
y
ax
3
+
bx
2
+
cx
+
d
có đồ thị như sau: Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bằng A. 4 B.
2
5
C. 2 D. 3
Đọc tiếp
Cho hàm số bậc ba y = ax 3 + bx 2 + cx + d có đồ thị như sau: Khoảng cách giữa hai điểm cực trị của đồ thị hàm số bằng
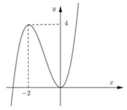
A. 4
B. 2 5
C. 2
D. 3
Tìm hệ số góc tiếp tuyến của đồ thị hàm số
y
−
x
3
−
3
x
2
+
2
tại điểm có hoành độ là nghiêṃ của phương trình y ¢¢ 0 A. 3 B. 2 C. 1 D. 4
Đọc tiếp
Tìm hệ số góc tiếp tuyến của đồ thị hàm số y = − x 3 − 3 x 2 + 2 tại điểm có hoành độ là nghiêṃ của phương trình y ¢¢ = 0
A. 3
B. 2
C. 1
D. 4
Cho hàm số yf(x) có đồ thị như hình vẽ bên. Biết rằng yf(x) là một trong bốn hàm được đưa ra trong các phương án dưới đây. Tìm yf(x) A.
f
x
−
x
4
+
2
x
2
B.
f
x
−
x
4
+
2
x...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Biết rằng y=f(x) là một trong bốn hàm được đưa ra trong các phương án dưới đây. Tìm y=f(x)
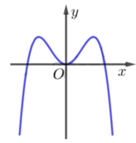
A. f x = − x 4 + 2 x 2
B. f x = − x 4 + 2 x 2 − 1
C. f x = x 4 + 2 x 2
D. f x = x 4 − 2 x 2
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? A.
-
2
x
+
1
2
x
+
1
B.
-
x
+
1
x...
Đọc tiếp
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?

A. - 2 x + 1 2 x + 1
B. - x + 1 x + 1
C. - x + 2 2 x + 1
D. - x x + 1