Đáp án C
Phương trình hoành độ giao điểm của (P) và d là 4 x + 4 x - 1 = x 2 - 1 ⇔ x ≠ 1 4 x + 4 = x 2 - 1 x - 1
⇔ x ≠ 1 x 3 - x 2 - 5 x - 3 = 0 ⇔ [ x = - 1 x = 3 Suy ra (P) và d có 2 điểm phân biệt
Đáp án C
Phương trình hoành độ giao điểm của (P) và d là 4 x + 4 x - 1 = x 2 - 1 ⇔ x ≠ 1 4 x + 4 = x 2 - 1 x - 1
⇔ x ≠ 1 x 3 - x 2 - 5 x - 3 = 0 ⇔ [ x = - 1 x = 3 Suy ra (P) và d có 2 điểm phân biệt
Cho hàm số f x = 3 2 x - 2 . 3 x có đồ thị như hình vẽ sau
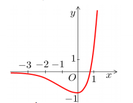
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại điểm có hoành độ là x = log 3 2
(2) Bất phương trình f x ≥ - 1 có nghiệm duy nhất.
(3) Bất phương trình f x ≥ 0 có tập nghiệm là - ∞ ; log 3 2
(4) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại 2 điểm phân biệt.
A. 2
B. 4
C. 1
D. 3
Cho hàm số f x = 3 2 x − 2.3 x có đồ thị như hình vẽ sau
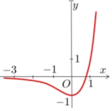
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y=0 cắt đồ thị hàm số (C) tại điểm có hoành độ là
x
=
log
3
2
(2) Bất phương trình
f
x
≥
−
1
có nghiệm duy nhất.
(3) Bất phương trình
f
x
≥
0
có tập nghiệm là
−
∞
;
log
3
2
(4) Đường thẳng y=0 cát đồ thị hàm số (C) tại 2 điểm phân biệt
A. 2.
B. 4.
C. 1.
D. 3.
Cho hàm số y=f(x) xác định trên R. Đồ thị hàm số y = f ' ( x ) cắt trục hoành tại 3 điểm a, b, c ( a < b < c ) như hình dưới:
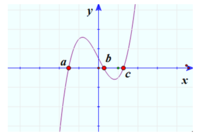
Biết f(b) < 0 Đồ thị hàm số y=f(x) cắt trục hoành tại bao nhiêu điểm phân biệt.
A. 4
B. 1
C. 0
D. 2
Cho a là một số thực dương khác 1. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau:
1. Hàm số y= l o g a x có tập xác định là D= ( 0 ; + ∞ ) .
2. Hàm số y= l o g a x là hàm đơn điệu trên khoảng ( 0 ; + ∞ ) .
3. Đồ thị hàm số y= l o g a x và đồ thị hàm số y = a x đối xứng nhau qua đường thẳng y= x.
4. Đồ thị hàm số y= l o g a x nhận Ox là một tiệm cận
A. 4
B. 1
C. 3
D. 2
Cho (C) là đồ thị của hàm số y = x - 2 x + 1 và đường thẳng d : y = m x + 1 . Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A. m ≥ 0
B. m < 0
C. m ≤ 0
D. m > 0
Có bao nhiêu số nguyên dương m sao cho đường thẳng y = x + m x cắt đồ thị hàm số y = 2 x − 1 x + 1 tại hai điểm phân biệt A, B và A B ≤ 4
A. 7
B. 6
C. 1
D. 2
Đồ thị hàm số y = ( x - 1 ) ( x 2 - 2 x + 4 ) cắt trục hoành tại bao nhiêu điểm
A. 0
B. 1
C. 2
D. 3
Đường thẳng x = k cắt đồ thị hàm số y = log 5 x và đồ thị hàm số y = log 3 ( x + 4 ) . Khoảng cách giữa các giao điểm là 1/2. Biết k = a + b , trong đó a, b là các số nguyên. Khi đó tổng a + b bằng
A. 7
B. 6
C. 8
D. 5
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.
Đồ thị (C) của hàm số y = x + 1 x - 1 và đường thẳng d: y=2x-1 cắt nhau tại hai điểm A và B khi đó độ dài đoạn AB bằng?
A. 2 3
B. 2 2
C. 2 5
D. 5