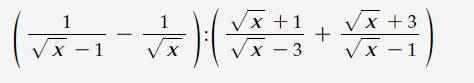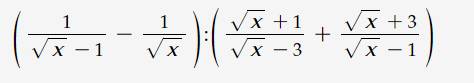\(G=1-\sqrt{x}-\dfrac{\sqrt{x}+x}{\sqrt{x}}\left(x>0\right).\)
\(G=\dfrac{\sqrt{x}-x-\sqrt{x}-x}{\sqrt{x}}=\dfrac{-2x}{\sqrt{x}}=-2\sqrt{x}.\)
\(G+x-8=0.\\ \Rightarrow-2\sqrt{x}+x-8=0.\\ \Leftrightarrow\left(\sqrt{x}-4\right)\left(\sqrt{x}+2\right)=0.\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=4.\\\sqrt{x}=-2\left(vôlý\right).\end{matrix}\right.\)
\(\Rightarrow x=16.\)
Tìm đk và rút gọn , tìm x để A < 0 , tính A biết x = 3-2
Tìm đk và rút gọn , tìm x để A < 0 , tính A biết x = 3-2\(\sqrt{2}\)
Cho A= \(\dfrac{\sqrt{x}+4}{{}\sqrt{x}-1}\) và B= \(\dfrac{x+2\sqrt{x}}{\sqrt{x}(\sqrt{x}+1)} -\dfrac{3\sqrt{x}-3}{x-1}\) (đk: x>0,x≠1)
a) Rút gọn P=A.B
b) Tìm x để P(\(\sqrt{x}+1\)) ≤ 6-x
c) Tìm x để P nhận giá trị nguyên
GIÚP MÌNH VỚI
Cho biểu thức: A= (√x/√x -3 + √x /√x+3): (1-3/√x+3) a) tìm đk để A có nghĩa b)rút gọn A c)Tìm x để A=-1
cho A = \(\left(\frac{x+3}{x-9}+\frac{1}{\sqrt{x}+3}\right):\frac{\sqrt{x}}{\sqrt{x}-3}\)ĐK: x > 0, x khác 9
a, rút gọn A
b, Tìm x thuộc Z để A thuộc Z
c, Tìm x để A >1/3
cho A = \(\left(\frac{x+3}{x-9}+\frac{1}{\sqrt{x}+3}\right):\frac{\sqrt{x}}{\sqrt{x}-3}\)ĐK: x > 0, x khác 9
a, rút gọn A
b, Tìm x thuộc Z để A thuộc Z
c, Tìm x để A >1/3
Cho biểu thức A = \(\dfrac{\sqrt{x}-2}{\sqrt{x}}\) và B = \(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{2x}{x-9}\) Đk: x>0, x≠9
a, Rút gọn B
b, Đặt P = A.B. Tìm giá trị nguyên nhỏ nhất của x để |P| > P.
cho bt
P=(\(\dfrac{1}{\sqrt{x}-1}\)-\(\dfrac{1}{\sqrt{x}}\)):(\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)-\(\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\))
a)Tìm đk của x để P xác định
b)Rút gọn P
c)Tìm xđể P=\(\dfrac{1}{4}\)
cho biểu thức A = \(\frac{\sqrt{x}+1}{\sqrt{x}-1}+\frac{\sqrt{x}-1}{\sqrt{x}+1}-\frac{3\sqrt{x}+1}{x-1}\)ĐK : x>= 0, x khác 1
a, rút gọn A
b, Tìm các giá trị của x để A bằng 1/2
c, Tìm các giá trị của x để A < 1
Q=\(\frac{2}{x-1}\)đk;x>0 ;x\(\ne\)1(phương trình này đã rút gọn r )
tìm số nguyên x lớn nhất để Q có gt là số nguyên.
