Các câu hỏi tương tự
Để đồ thị hàm số
y
-
x
4
-
(
m
-
3
)
x
2
+
m
+
1
có điểm cực đại mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là: A.
m
≥
3
B. m 3. C.
m
≤
3
D. m 3
Đọc tiếp
Để đồ thị hàm số y = - x 4 - ( m - 3 ) x 2 + m + 1 có điểm cực đại mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là:
A. m ≥ 3
B. m > 3.
C. m ≤ 3
D. m < 3
Cho đồ thị hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
có điểm cực đại là A(-2;2), điểm cực tiểu là B(0;-2). Tìm tất cả các giá trị của m để phương trình
a
x
3
+
b
x
2
+
c
x
+
d
m
có 3 nghiệm phân biệt. A.
m
2
B.
m...
Đọc tiếp
Cho đồ thị hàm số y = a x 3 + b x 2 + c x + d có điểm cực đại là A(-2;2), điểm cực tiểu là B(0;-2). Tìm tất cả các giá trị của m để phương trình a x 3 + b x 2 + c x + d = m có 3 nghiệm phân biệt.
A. m > 2
B. m < - 2
C. - 2 < m < 2
D. m = 2 m = - 2
Cho hàm số: yx-3-3(m+1)x2+9x+m-2 (1) có đồ thị là (Cm). Có bao nhiêu giá trị nguyên của tham số m để (Cm) có điểm cực đại, cực tiểu đối xứng với nhau qua đường thẳng y1/2x ? A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Cho hàm số: y=x-3-3(m+1)x2+9x+m-2 (1) có đồ thị là (Cm). Có bao nhiêu giá trị nguyên của tham số m để (Cm) có điểm cực đại, cực tiểu đối xứng với nhau qua đường thẳng y=1/2x ?
A. 0
B. 1
C. 2
D. 3
Cho hàm số bậc ba yf(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số
y
f
(
x
-
1
)
-
m
-
1
có 3 điểm cực trị? A. -1m5 B.
-
1
≤
m
≤
5
C.
m...
Đọc tiếp
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f ( x - 1 ) - m - 1 có 3 điểm cực trị?
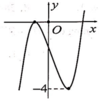
A. -1<m<5
B. - 1 ≤ m ≤ 5
C. m ≥ - 1 hoặc m ≤ - 5
D. m>-1 hoặc m<-5
Cho hàm số bậc ba y f(x) có đồ thị như hình bên. Tất cả các giá trị của tham số m để hàm số y |f(x)+m| có 3 điểm cực trị là: A. m
≤
-1 hoặc m
≥
3 B. m
≤
-3 hoặc m
≥
1 C. m -1 hoặc m 3 D. 1
≤
m
≤
3
Đọc tiếp
Cho hàm số bậc ba y = f(x) có đồ thị như hình bên. Tất cả các giá trị của tham số m để hàm số y = |f(x)+m| có 3 điểm cực trị là:
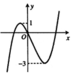
A. m ≤ -1 hoặc m ≥ 3
B. m ≤ -3 hoặc m ≥ 1
C. m = -1 hoặc m = 3
D. 1 ≤ m ≤ 3
Cho hàm số
y
x
3
+
(
m
+
3
)
x
2
-
(
2
m
+
9
)
x
+
m
+
6
có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để (C) có hai điểm cực trị và khoảng cách từ gốc toạ độ O đến đường thẳng nối hai điểm cực trị là lớn nhất. A. m
-...
Đọc tiếp
Cho hàm số y = x 3 + ( m + 3 ) x 2 - ( 2 m + 9 ) x + m + 6 có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để (C) có hai điểm cực trị và khoảng cách từ gốc toạ độ O đến đường thẳng nối hai điểm cực trị là lớn nhất.
A. m = - 6 ± 3 2 2
B. m = - 3 ± 3 2 2
C. m = - 3 ± 6 2
D. m = - 6 ± 6 2
Cho hàm số bậc ba y f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số
y
f
x
+
m
có 3 điểm cực trị? A.
1
≤
m
≤
3
B. m -1 hoặc m 3 C.
m
≤
-
1
h
o
ặ
c
m
≥
3
D. ...
Đọc tiếp
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên. Tất cả giá trị thực của tham số m để hàm số y = f x + m có 3 điểm cực trị?
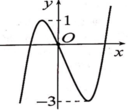
A. 1 ≤ m ≤ 3
B. m = -1 hoặc m = 3
C. m ≤ - 1 h o ặ c m ≥ 3
D. m ≤ - 3 hoặc m ≥ 1
Cho hàm số
y
x
4
-
2
(
1
-
m
2
)
x
2
+
m
+
1
. Tìm tất cả các giá trị của tham số m để hàm số có...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( 1 - m 2 ) x 2 + m + 1 . Tìm tất cả các giá trị của tham số m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất
A. m = 0
B. m = - 1 2
C. m = 1
D. m = 1 2
Để đồ thị hàm số
y
x
4
+
(
2
m
+
3
)
x
2
+
m
2
-
4
có đúng một điểm cực trị thì tất cả giá trị thực của tham số m là: A.
m
≥
-
3
2
B.
m
-
3
2
C. ...
Đọc tiếp
Để đồ thị hàm số y = x 4 + ( 2 m + 3 ) x 2 + m 2 - 4 có đúng một điểm cực trị thì tất cả giá trị thực của tham số m là:
A. m ≥ - 3 2
B. m > - 3 2
C. m ≤ - 3 2
D. m < - 3 2




