Question

    đề : C/m DFMH là hình bình hành

giúp e với ạ

Answer 1

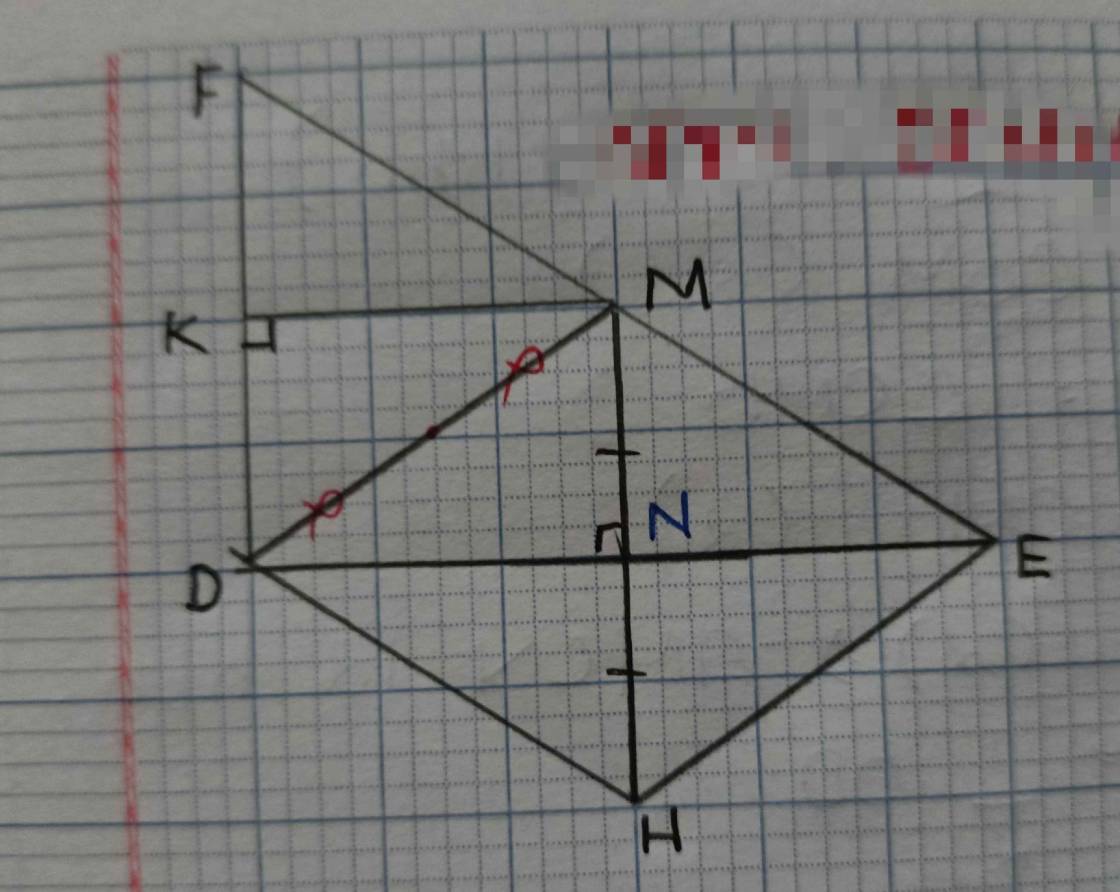
a: Xét tứ giác DNMK có

\(\widehat{DNM}=\widehat{DKM}=\widehat{KDN}=90^0\)

=>DNMK là hình chữ nhật

b: Xét ΔDEF có NM//DF

nên \(\dfrac{NM}{DF}=\dfrac{EM}{EF}=\dfrac{1}{2}\)

=>\(NM=\dfrac{1}{2}DF\)

mà \(NM=\dfrac{1}{2}MH\)

nên MH=DF

Xét tứ giác DFMH có

MH//DF

MH=DF

Do đó: DFMH là hình bình hành

=>DM cắt FH tại trung điểm của mỗi đường

mà O là trung điểm của DM

nên O là trung điểm của FH

=>F,O,H thẳng hàng

c:

Xét ΔDEF có

M là trung điểm của EF

MN//DF
Do đó: N là trung điểm của DE

Xét ΔDEF có

M là trung điểm của FE

MK//DE

Do đó: K là trung điểm của DF

Để DNMK là hình vuông thì DN=DK

mà \(DN=\dfrac{DE}{2}\) và \(DK=\dfrac{DF}{2}\)

nên DE=DF