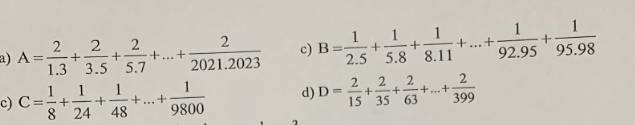a: \(A=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2021\cdot2023}\)
\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\)
\(=1-\dfrac{1}{2023}=\dfrac{2022}{2023}\)
b: \(B=\dfrac{1}{2\cdot5}+\dfrac{1}{5\cdot8}+...+\dfrac{1}{92\cdot95}+\dfrac{1}{95\cdot98}\)
\(=\dfrac{1}{3}\left(\dfrac{3}{2\cdot5}+\dfrac{3}{5\cdot8}+...+\dfrac{3}{92\cdot95}+\dfrac{3}{95\cdot98}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{92}-\dfrac{1}{95}+\dfrac{1}{95}-\dfrac{1}{98}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{2}-\dfrac{1}{98}\right)=\dfrac{1}{3}\cdot\dfrac{48}{98}=\dfrac{16}{98}=\dfrac{8}{49}\)
c: \(C=\dfrac{1}{8}+\dfrac{1}{24}+\dfrac{1}{48}+...+\dfrac{1}{9800}\)
\(=\dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+\dfrac{1}{6\cdot8}+...+\dfrac{1}{98\cdot100}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+...+\dfrac{2}{98\cdot100}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{98}-\dfrac{1}{100}\right)\)
\(=\dfrac{1}{2}\cdot\left(\dfrac{1}{2}-\dfrac{1}{100}\right)=\dfrac{1}{2}\cdot\dfrac{49}{100}=\dfrac{49}{200}\)
d: \(D=\dfrac{2}{15}+\dfrac{2}{35}+...+\dfrac{2}{399}\)
\(=\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{19\cdot21}\)
\(=\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{19}-\dfrac{1}{21}\)
\(=\dfrac{1}{3}-\dfrac{1}{21}=\dfrac{6}{21}=\dfrac{2}{7}\)