o: x^4+x^3+x^2-1
=x^3(x+1)+(x-1)(x+1)
=(x+1)(x^3+x-1)
q: \(=\left(x^3-y^3\right)+xy\left(x-y\right)\)
=(x-y)(x^2+xy+y^2)+xy(x-y)
=(x-y)(x^2+2xy+y^2)
=(x-y)(x+y)^2
s: =(2xy)^2-(x^2+y^2-1)^2
=(2xy-x^2-y^2+1)(2xy+x^2+y^2-1)
=[1-(x^2-2xy+y^2]+[(x+y)^2-1]
=(1-x+y)(1+x-y)(x+y-1)(x+y+1)
u: =(x^2-y^2)-4(x+y)
=(x+y)(x-y)-4(x+y)
=(x+y)(x-y-4)
x: =(x^3-y^3)-(3x-3y)
=(x-y)(x^2+xy+y^2)-3(x-y)
=(x-y)(x^2+xy+y^2-3)
z: =3(x-y)+(x^2-2xy+y^2)
=3(x-y)+(x-y)^2
=(x-y)(x-y+3)
o) \(x^4+x^3+x^2-1\)
\(=\left(x^4+x^3\right)+\left(x^2-1\right)\)
\(=x^3\left(x+1\right)+\left(x+1\right)\left(x-1\right)\)
\(=\left(x+1\right)\left(x^3+x-1\right)\)
q) \(x^3+x^2y-xy^2-y^3\)
\(=\left(x^3+x^2y\right)-\left(xy^2+y^3\right)\)
\(=x^2\left(x+y\right)-y^2\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-y^2\right)\)
\(=\left(x+y\right)^2\left(x-y\right)\)
s) \(4x^2y^2-\left(x^2+y^2-1\right)^2\)
\(=\left(2xy\right)^2-\left(x^2+y^2-1\right)^2\)
\(=\left(2xy-x^2-y^2+1\right)\left(2xy+x^2+y^2-1\right)\)
\(=-\left(x^2-2xy+y^2-1\right)\left(x^2+2xy+y^2-1\right)\)
\(=-\left(x-y-1\right)\left(x-y+1\right)\left(x+y+1\right)\left(x+y-1\right)\)
u) \(x^2-y^2-4x-4y\)
\(=\left(x^2-y^2\right)-\left(4x+4y\right)\)
\(=\left(x+y\right)\left(x-y\right)-4\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-4\right)\)
x) \(x^3-y^3-3x+3y\)
\(=\left(x^3-y^3\right)-\left(3x-3y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2-3\right)\)
z) \(3x-3y+x^2-2xy+y^2\)
\(=\left(3x-3y\right)+\left(x^2-2xy+y^2\right)\)
\(=3\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3+x-y\right)\)

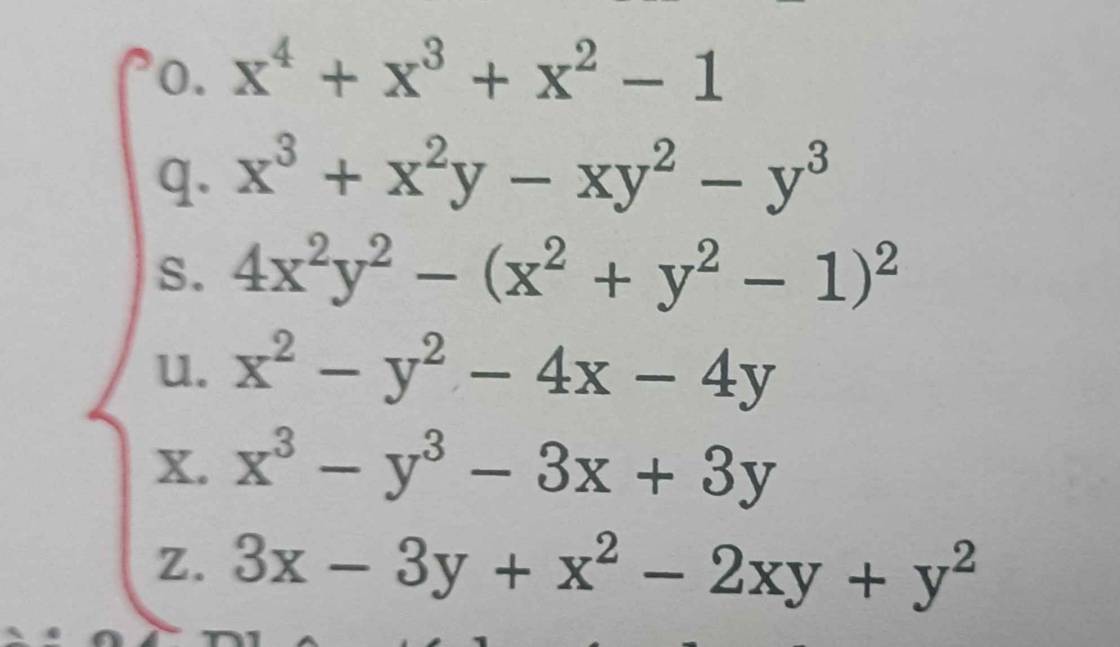










 \
\



