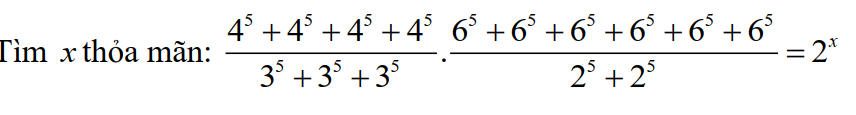Question

Đề bài dài quá nên mn nhìn ảnh nhé

Answer 1

\(\dfrac{4^5+4^5+4^5+4^5}{3^5+3^5+3^5}.\dfrac{6^5+6^5+6^5+6^5+6^5+6^5}{2^5+2^5}\)

\(=\dfrac{4.4^5}{3.3^5}.\dfrac{6.6^5}{2.2^5}=\dfrac{4^6}{3^6}.\dfrac{6^6}{2^6}=\left(\dfrac{6}{3}\right)^6.\left(\dfrac{4}{2}\right)^6=2^{12}\)

\(\Rightarrow2^x=2^{12}\Rightarrow x=12\)

Answer 2

a) \(\dfrac{4^5+4^5+4^5+4^5}{3^5+3^5+3^5}\cdot\dfrac{6^5+6^5+6^5+6^5+6^5+6^5}{2^5+2^5}=2^x\)

\(\Leftrightarrow\cdot\dfrac{4^6.6^6}{3^6.2^6}=2^x\)

\(=>\left(\dfrac{4}{2}\right)^6.\left(\dfrac{6}{3}\right)^6=2^x\)

\(=>2^6.2^6=2^x\)

\(2^{12}=2^x\)

`=>x=12`

Vậy `x=12`