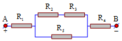
Bài 1:
Mạch điện gồm: [(\(R_1\) // \(R_2\) ) nt (\(R_3\) // \(R_4\) )]
\(R_{AB}=R_{12}+R_{34}\)
\(\rArr R_{AB}=\frac{2.3}{2+3}+\frac{4.6}{4+6}=1,2+2,4=3,6\left(\Omega\right)\)
\(I_{AB}=I_{12}=I_{34}=\frac{U_{AB}}{R_{AB}}=\frac{18}{3,6}=5\left(A\right)\)
\(U_{34}=U_3=I_{34}.R_{34}=5.2,4=12\left(V\right)\)
\(I_3=\frac{U_3}{R_3}=\frac{12}{4}=3\left(A\right)\)
Vậy \(I_3=3A\)
Bài 2:
Mạch điện gồm [\(R_1\) nt\(R_{}\) ]
\(R_{AB}=R_1+R=6+R\)
\(I_{AB}=I_{R}=\frac{U_{AB}}{R_{AB}}=\frac{12}{6+R}\)
Ta có: \(P_{R}=I_{R}^2.R\)
\(\rArr P_{R}=\left(\frac{12}{6+R}\right)^2.R\)
\(\rArr P_{R}=\frac{12^2}{\frac{6^2}{R}+R+2.6}\)
\(\rArr P_{R}=\frac{144}{\frac{36}{R}+R+12}\)
Ta thấy \(\frac{36}{R}+R\ge2.\sqrt{\frac{36}{R}.R}\)
\(\rArr\frac{36}{R}+R\ge2.6\)
\(\rArr\frac{36}{R}+R\ge12\)
\(\rArr\) Mẫu số \(\ge12+12\)
\(\rArr\) Mẫu số \(\ge24\)
\(\rArr P_{R}\max=\frac{144}{24}=6\lrArr\frac{36}{R}=R\lrArr R=6\Omega\)
Vậy \(P_{R}\max=6WkhiR=6\Omega\)