Các câu hỏi tương tự
Cho hàm số
f
(
x
)
1
/
(
x
-
2
)
có đồ thị như ở Hình 52Quan sát đồ thị và cho biết:- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị nào. - Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị nào.
Đọc tiếp
Cho hàm số f ( x ) = 1 / ( x - 2 ) có đồ thị như ở Hình 52
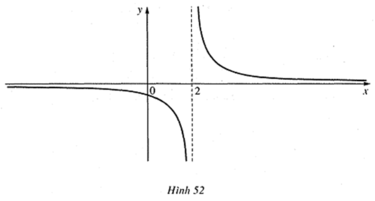
Quan sát đồ thị và cho biết:
- Khi biến x dần tới dương vô cực, thì f(x) dần tới giá trị nào.
- Khi biến x dần tới âm vô cực, thì f(x) dần tới giá trị nào.
Cho dãy số
(
u
n
)
thoả mãn điều kiện: Với mọi
n
∈
N
∗
thì
0
u
n
1
v
à
u
n
+
1
1
-
1...
Đọc tiếp
Cho dãy số ( u n ) thoả mãn điều kiện: Với mọi n ∈ N ∗ thì 0 < u n < 1 v à u n + 1 < 1 - 1 4 u n Chứng minh dãy số đã cho là dãy giảm.
Xét hàm số
f
x
2
x
2
-
2
x
x
-
1
1. Cho biến x những giá trị khác 1 lập thành dãy số
x
n
,
x
n...
Đọc tiếp
Xét hàm số f x = 2 x 2 - 2 x x - 1
1. Cho biến x những giá trị khác 1 lập thành dãy số x n , x n → 1 như trong bảng sau:

Khi đó, các giá trị tương ứng của hàm số
f ( x 1 ) , f ( x 2 ) , … , f ( x n ) , …
cũng lập thành một dãy số mà ta kí hiệu là f ( x n ) .
a) Chứng minh rằng f ( x n ) = 2 x n = ( 2 n + 2 ) / n .
b) Tìm giới hạn của dãy số f ( x n ) .
2. Chứng minh rằng với dãy số bất kì x n , x n ≠ 1 và x n → 1 , ta luôn có f ( x n ) → 2 .
(Với tính chất thể hiện trong câu 2, ta nói hàm số f x = 2 x 2 - 2 x x - 1 có giới hạn là 2 khi x dần tới 1).
Cho số nguyên dương n thỏa mãn điều kiện
720
(
C
7
7
+
C
8
7
+
.
.
.
C
n
7
)
1
4032
A
n
+
1
10...
Đọc tiếp
Cho số nguyên dương n thỏa mãn điều kiện 720 ( C 7 7 + C 8 7 + . . . C n 7 ) = 1 4032 A n + 1 10 . Hệ số của x 7 trong khai triển x - 1 x 2 n x ≠ 0
![]()
![]()
![]()
![]()
Tìm hệ số của x trong khai triển
P
x
1
+
n
4
x
-
3
n
8
x
3
n
-...
Đọc tiếp
Tìm hệ số của x trong khai triển P x = 1 + n 4 x - 3 n 8 x 3 n - 4 với x > 0 . Biết n là số nguyên dương thỏa mãn điều kiện A n 2 + 3 C n n - 2 - C n + 1 3 = A n + 1 2 - 2 n .
A. 28
B. 78
C. 218
D. 80
Cho hai dãy số
(
u
n
)
và
(
v
n
)
. Biết
l
i
m
u
n
−
∞
và
v
n
≤
u
n
với mọi n. Có kết luận gì về giới hạn của dãy
(
v
n...
Đọc tiếp
Cho hai dãy số ( u n ) và ( v n ) . Biết l i m u n = − ∞ và v n ≤ u n với mọi n. Có kết luận gì về giới hạn của dãy ( v n ) khi n → + ∞ ?
Có nhiều tờ giấy chồng nhau, mỗi tờ có bề dày là 0,1 mm. Ta xếp chồng liên tiếp tờ này lên tờ khác (h.48). Giả sử có thể thực hiện việc xếp giấy như vậy một cách vô hạn.Gọi u1 là bề dày của một tờ giấy,
u
2
là bề dày của một xếp giấy gồm hai tờ,
u
3
là bề dày của một xếp giấy gồm ba tờ, …,
u
n
là bề dày của một xếp giấy gồm n tờ. Tiếp tục như vậy t được dãy số vô...
Đọc tiếp
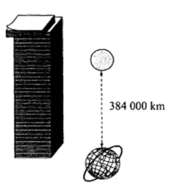
Có nhiều tờ giấy chồng nhau, mỗi tờ có bề dày là 0,1 mm. Ta xếp chồng liên tiếp tờ này lên tờ khác (h.48). Giả sử có thể thực hiện việc xếp giấy như vậy một cách vô hạn.
Gọi u1 là bề dày của một tờ giấy, u 2 là bề dày của một xếp giấy gồm hai tờ, u 3 là bề dày của một xếp giấy gồm ba tờ, …, u n là bề dày của một xếp giấy gồm n tờ. Tiếp tục như vậy t được dãy số vô hạn ( u n ).
Bảng sau đây cho biết bề dày (tính theo mm) của một số chồng giấy.

a) Quan sát bảng trên và nhận xét về giá trị của u n khi n tăng lên vô hạn.
b) Với n như thế nào thì ta đạt được những chồng giấy có về dày lớn hơn khoảng cách từ Trái Đất tới Mặt Trăng? (Cho biết khoảng cách này ở một thời điểm xác định là 384000 km hay 384 . 10 9 m m
Cho số nguyên dương n thỏa mãn điều kiện: 720
C
7
7
+
C
8
7
+
C
9
7
+...
Đọc tiếp
Cho số nguyên dương n thỏa mãn điều kiện: 720 C 7 7 + C 8 7 + C 9 7 + . . . + C n 7 = 1 4032 A n + 1 10 . Hệ số của x 7 trong khai triển x - 1 x 2 n ( x ≠ 0 ) bằng:
A. -120
B. -560
C. 120
D. 560
Cho hai dãy số
u
n
và
v
n
. Biết
|
u
n
–
2
|
≤
v
n
với mọi n và
l
i
m
v
n
0
. Có kết luận gì về giới hạn...
Đọc tiếp
Cho hai dãy số u n và v n . Biết | u n – 2 | ≤ v n với mọi n và l i m v n = 0 . Có kết luận gì về giới hạn của dãy số u n ?