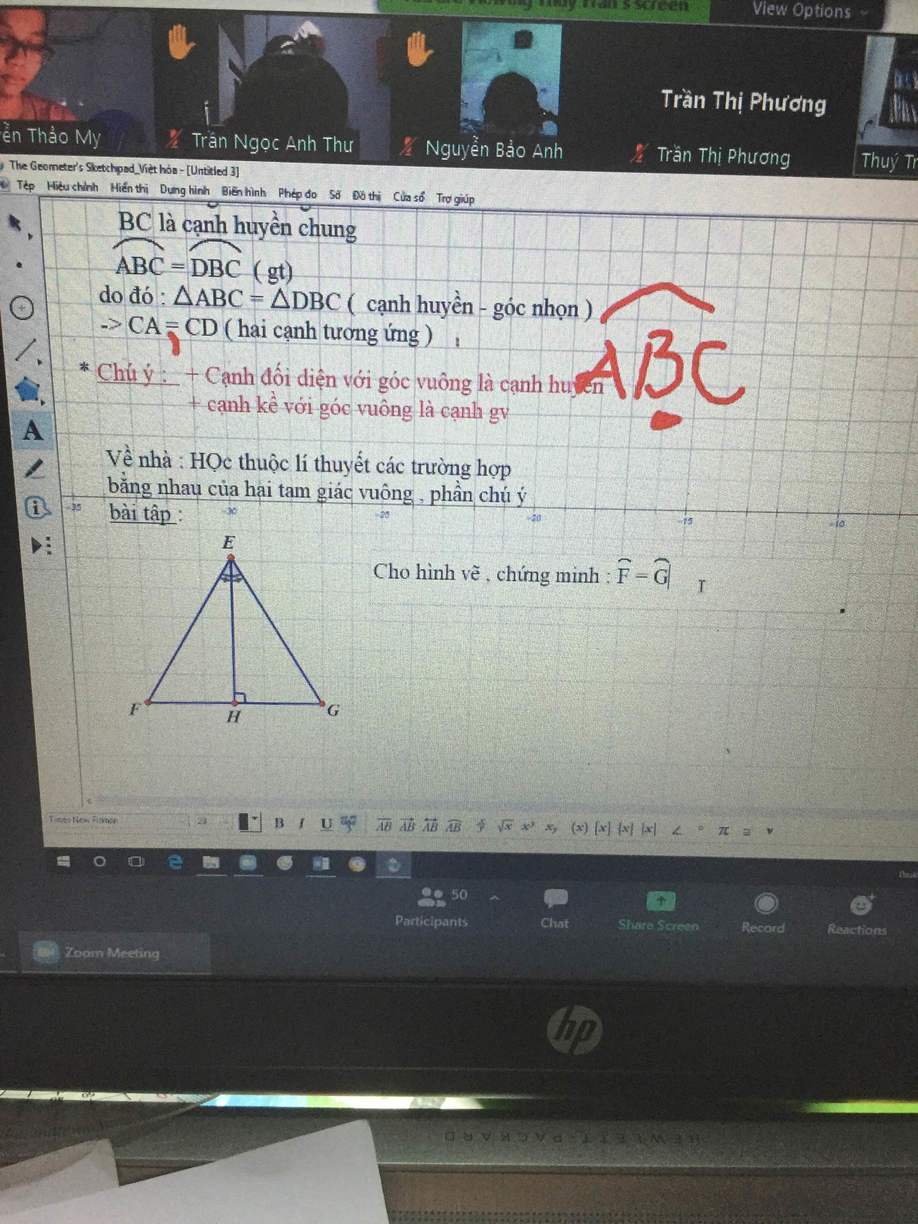
Xét tg EFH và tg EGH, có:
\(\left\{{}\begin{matrix}\widehat{FEH}=\widehat{GEH}\left(gt\right)\\EH:canh\cdot chung\\\widehat{EHF}=\widehat{EHG}\left(=90^0\right)\end{matrix}\right.\)
\(=>\Delta EFH=\Delta EGH\left(g\cdot c\cdot g\right)\)
\(=>\widehat{F}=\widehat{G}\left(cgtu\right)\)
Xét ΔEHF và ΔEHG có:
\(\widehat{EHF}=\widehat{EHG}\left(=90^o\right)\)
Chung EH
\(\widehat{FEH}=\widehat{GEH}\left(gt\right)\)
⇒ΔEHF = ΔEHG (g.c.g)
⇒\(\widehat{F}=\widehat{G}\) (2 góc tương ứng)







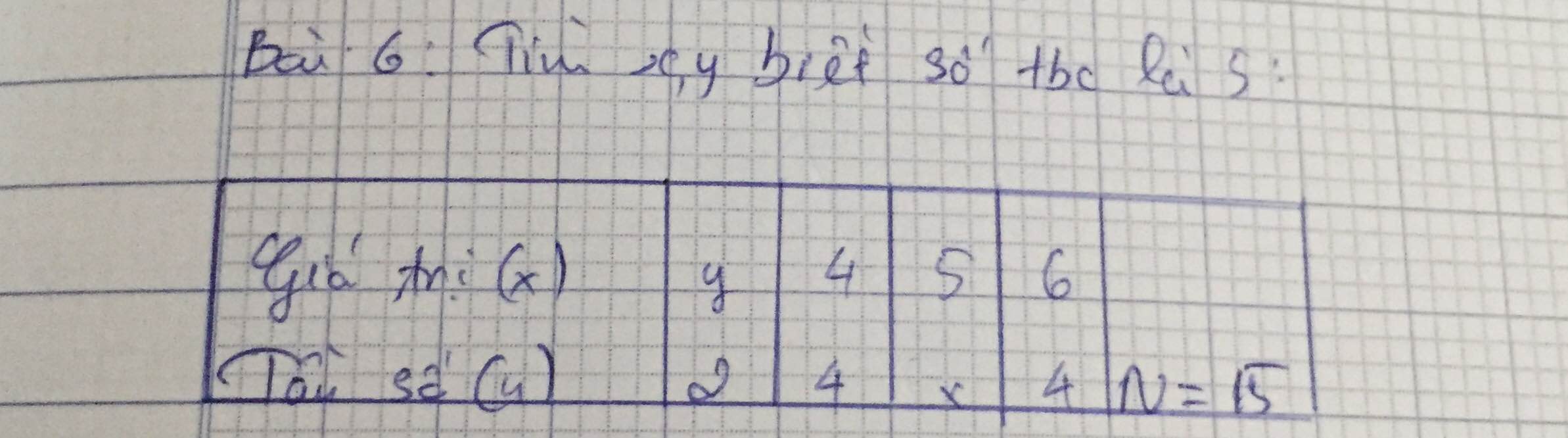









 GIÚP TỚ VỚI MAI NỘP RỒI
GIÚP TỚ VỚI MAI NỘP RỒI