\(x^2+y^3-3y^2+3y-1=5\)
\(\Leftrightarrow x^2+\left(y-1\right)^3=5\)
\(\Leftrightarrow\left(y-1\right)^3=5-x^2\)
Do y là số tự nhiên \(\Rightarrow y\ge0\Rightarrow y-1\ge-1\)
\(\Rightarrow\left(y-1\right)^3\ge-1\)
Đồng thời \(x^2\ge0\Rightarrow5-x^2\le5\)
\(\Rightarrow-1\le\left(y-1\right)^3\le5\)
Mà \(\left(y-1\right)^3\) là lập phương của 1 số nguyên
\(\Rightarrow\left[{}\begin{matrix}\left(y-1\right)^3=-1\\\left(y-1\right)^3=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=0\\y=2\end{matrix}\right.\)
- Với \(y=0\Rightarrow x^2+\left(0-1\right)^3=5\Rightarrow x^2=6\) (ko có x tự nhiên thỏa mãn)
- Với \(y=2\Rightarrow x^2+\left(2-1\right)^3=5\Rightarrow x^2=4\)
\(\Rightarrow x=2\)
Vậy \(x=y=2\)






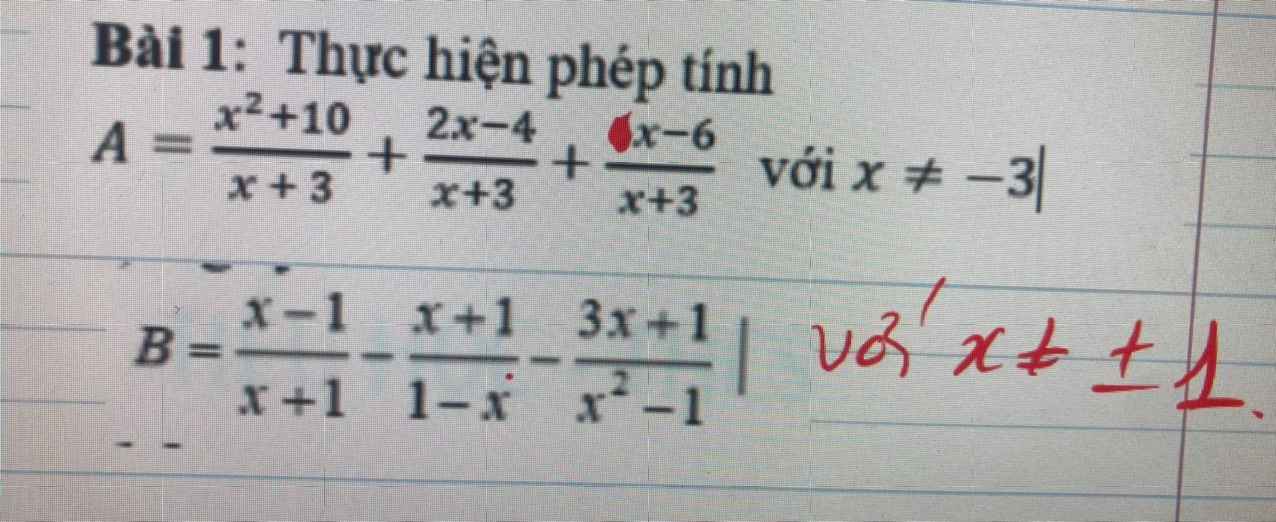







 Cứu
Cứu 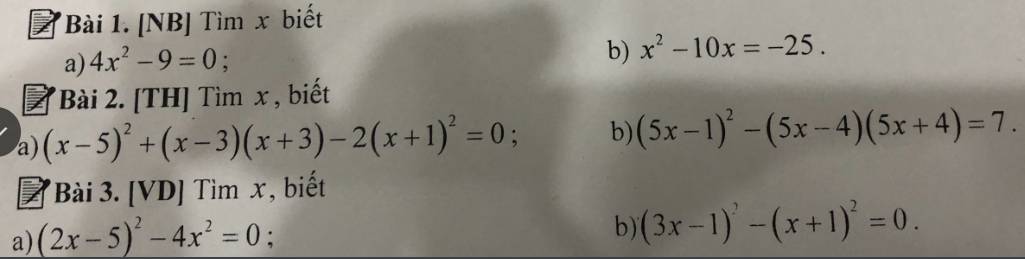



 cứu với
cứu với