Bài 2:
\(a,\left(\dfrac{x}{2}-4\right)^2\\ =\dfrac{x^2}{4}-2\cdot\dfrac{x}{2}\cdot4+4^2\\ =\dfrac{x^2}{4}-4x+16\\ b,\left(\dfrac{1}{y}+\dfrac{y}{x}\right)^2\\ =\dfrac{1}{y^2}+\dfrac{2}{x}+\dfrac{y^2}{x^2}\\ c,\left(5x-8y\right)\left(5x+8y\right)\\ =25x^2-64y^2\\ d,\left(x+y-2\right)^2\\ =x^2+y^2+4+2xy-4x-4y\)
Bài 3:
\(a,9x^2-25\\ =\left(3x\right)^2-5^2\\ =\left(3x-5\right)\left(3x+5\right)\\ b,2xy^2+x^2y^4+1\\ =\left(xy^2\right)^2+2\cdot xy^2\cdot1+1^2\\ =\left(xy^2+1\right)^2\\ c,16x^4-y^8\\ =\left(4x^2\right)^2-\left(y^4\right)^2\\ =\left(4x^2-y^2\right)\left(4x^2+y^2\right)\\ =\left(4x^2+y^2\right)\left(2x+y\right)\left(2x-y\right)\\ d,4x^4+1-4x^2\\ =\left(2x^2\right)^2-2\cdot2x^2\cdot1+1^2\\ =\left(2x^2-1\right)^2\)


 Cứu
Cứu 





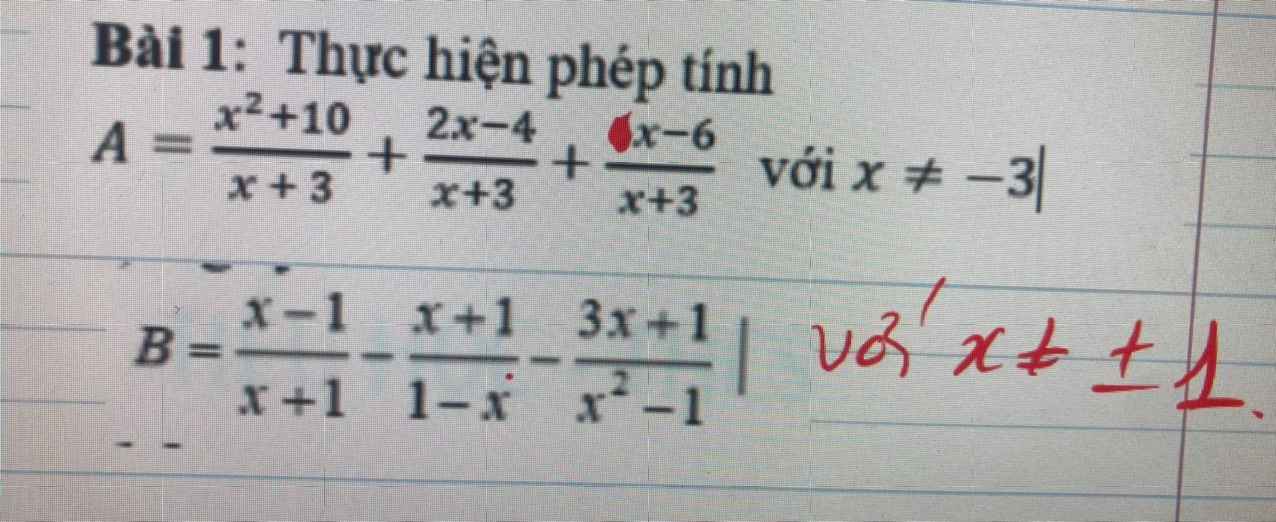






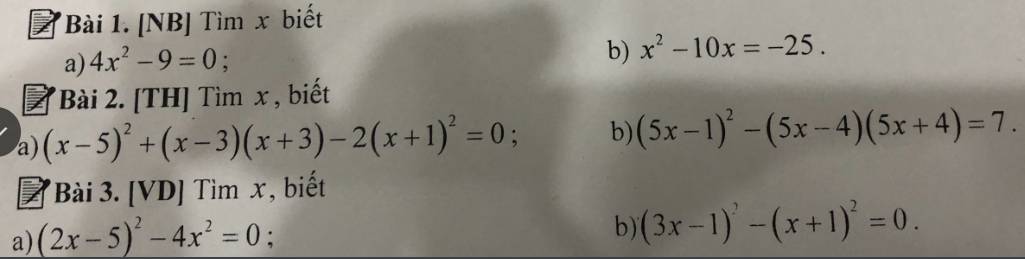



 cứu với
cứu với