a: Xét tứ giác AEHF có \(\hat{AEH}+\hat{AFH}=90^0+90^0=180^0\)
nên AEHF là tứ giác nội tiếp
b: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
\(\hat{DBH}\) chung
Do đó: ΔBDH~ΔBEC
=>\(\frac{BD}{BE}=\frac{BH}{BC}\)
=>\(BH\cdot BE=BD\cdot BC\)
Xét ΔCDH vuông tại D và ΔCFB vuông tại F có
\(\hat{DCH}\) chung
Do đó: ΔCDH~ΔCFB
=>\(\frac{CD}{CF}=\frac{CH}{CB}\)
=>\(CH\cdot CF=CD\cdot CB\)
\(CH\cdot CF+BH\cdot BE\)
\(=BD\cdot BC+CD\cdot BC=BC\cdot\left(BD+CD\right)=BC^2\)
















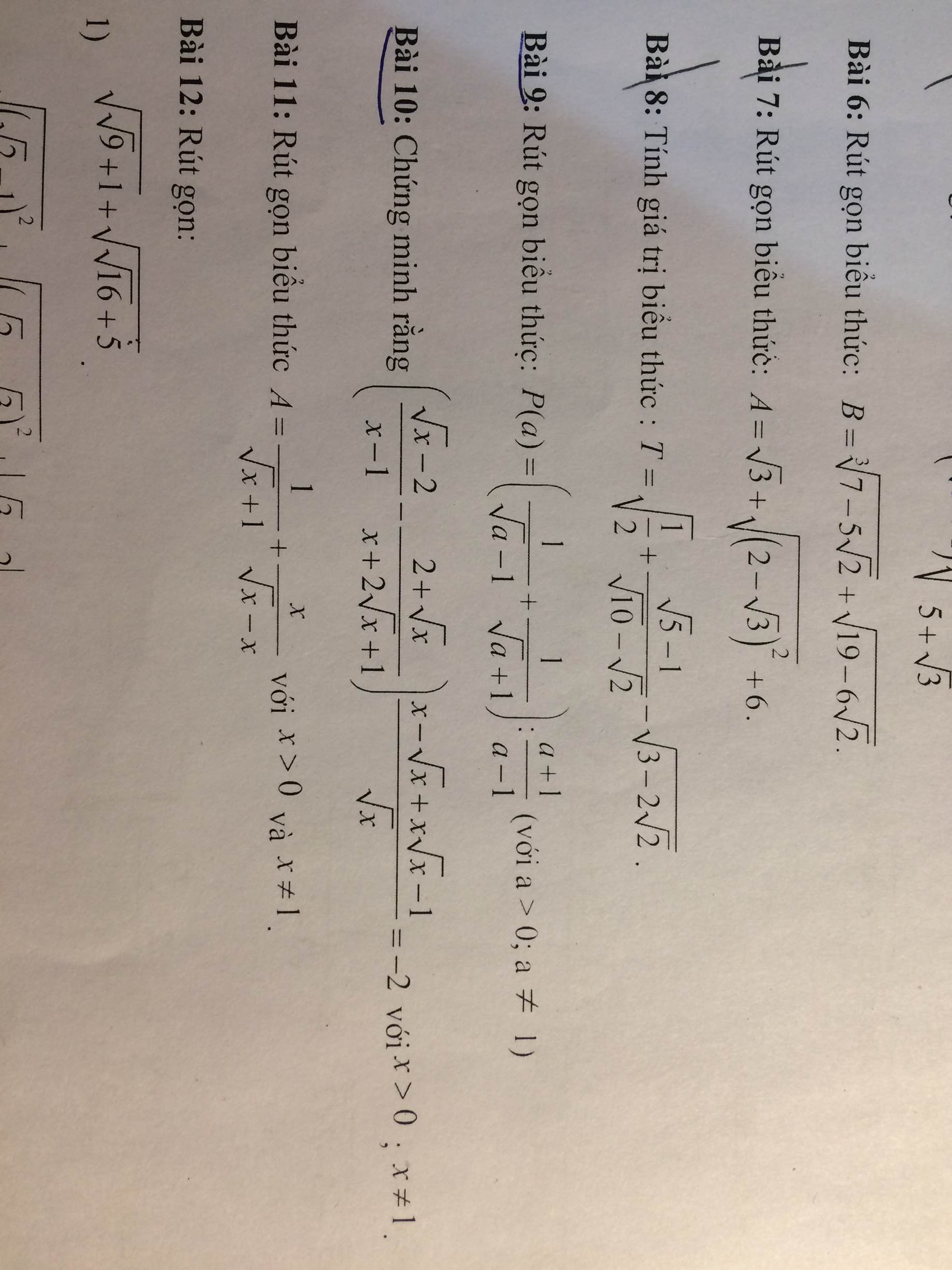






 Giải giúp mik câu này ạ ngày may mik thi r 🥺
Giải giúp mik câu này ạ ngày may mik thi r 🥺
