Ta có:
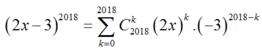
do đó khai triển trên có 2019 số hạng.
Chọn A.
Ta có:
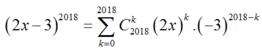
do đó khai triển trên có 2019 số hạng.
Chọn A.
Trong khai triển nhị thức Niu tơn của P x = 2 3 x + 3 2018 thành đa thức, có tất cả bao nhiêu số hạng có hệ số nguyên dương?
A. 673
B. 675
C. 674
D. 672
Có bao nhiêu số hạng trong khai triển nhị thức 2 x - 3 2018
A. 2018.
B. 2020.
C. 2019.
D. 2017.
Trong khai triển nhị thức Niutơn của a + 2 n + 6 có tất cả 2019 số hạng . Khi đó giá trị n bằng
A. 2012
B. 2013
C. 2018
D. 2019
Cho nhị thức x + 1 x n , x ≠ 0 trong tổng số các hệ số của khai triển nhị thức đó là 1024. Khi đó số hạng không chứa x trong khai triển nhị thức đã cho bằng
A. 252
B. 125
C. -252
D. 525
Biết rằng khi khai triển nhị thức Niutơn x + 1 2 x 4 n = a 0 x n + a 1 x n - 1 . 1 x 4 + a 2 x n - 2 . 1 x 4 2 + a 3 x n - 3 . 1 x 4 3 . . . (với n là số nguyên lớn hơn 1) thì ba số a 0 , a 1 , a 2 theo thứ tự lập thành một cấp số cộng. Hỏi trong khai triển trên, có bao nhiêu số hạng mà lũy thừa của x là một số nguyên.
A. 1
B. 2
C. 3
D. 4
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525
Hệ số chứa x 2 trong khai triển nhị thức của đa thức f x = x − 2 x n x > 0 ; n ∈ ℕ * bằng bao nhiêu, biết 2 A n 2 − C n 2 = n 2 + 5 .
A. 40.
B. -80.
C. 90.
D. -32.
Hệ số chứa x 2 trong khai triển nhị thức của đa thức f ( x ) = x − 2 x n x > 0 ; n ∈ ℕ * bằng bao nhiêu, biết 2 A n 2 − C n 2 = n 2 + 5 .
A. 40
B. -80
C. 90
D. -32
Gọi a 2018 là hệ số của số hạng chứa x 2018 trong khai triển nhị thức Niutơn x − x n với x ≥ 0 ; n là số nguyên dương thỏa mãn 1 2 ! .2017 ! + 1 4 ! .2015 ! + 1 6 ! .2013 ! ... + 1 2016 ! .3 ! + 1 2018 ! = 2 2018 − 1 P n . Tìm a 2018
A. 2017
B. − C 2018 3 .
C. 2019
D. C 2019 2 .