Chọn D
Có vô số phép tịnh tiến biến một đường thẳng d thành chính nó. Khi đó, vecto tịnh tiến có giá song song hoặc trùng với đường thẳng d.
Chọn D
Có vô số phép tịnh tiến biến một đường thẳng d thành chính nó. Khi đó, vecto tịnh tiến có giá song song hoặc trùng với đường thẳng d.
I. Trắc nghiệm (5 điểm)
Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó?
A. Không có
B. 1
C. 2
D. Vô số
Trong mặt phẳng Oxy, cho đường thẳng d: y=3x-2 để phép tịnh tiến theo v → biến đường thẳng d thành chính nó thì
A. v → = − 1 ; − 3
B. v → = − 1 ; 3
C. v → = 3 ; 1
D. v → = 3 ; - 1
Cho hai parabol P 1 : y = x 2 + 3 x − 2 và P 2 : y = x 2 + 5 x + 4 . Phép tịnh tiến theo v → = a ; b biến P 1 thành P 2 thì a+b bằng
A. 3
B. -3
C. -1
D. 1
Có thể chia một hình lập phương thành bao nhiêu tứ diện bằng nhau
A. Hai B. Vô số
C. Bốn D. Sáu.
Chứng minh rằng phép vị tự biến mỗi đường thẳng thành một đường thẳng song song hoặc trùng với nó, biến mỗi mặt phẳng thành một mặt phẳng song song hoặc trùng với mặt phẳng đó.
Cho đường tròn (C) và điểm A nằm ngoài mặt phẳng chứa (C). Có tất cả bao nhiêu mặt cầu chứa đường tròn (C) và đi qua A?
A. 0 B. 1
C. 2 D. Vô số
Từ thành phố A có 10 con đường đến thành phố B. Từ thành phố A có 9 con đường đến thành phố C. Từ thành phố B có 6 con đường đến thành phố D. Từ thành phố C có 11 con đường đến thành phố D. Không có con đường nào nối B với C. Hỏi có bao nhiêu cách đi từ A đến D?
A. 156
B. 157
C. 159
D. 176
Phương trình sau có bao nhiêu nghiệm:
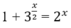
A. 0 B. 1
C. 2 D. Vô số
Phương trình sau có bao nhiêu nghiệm: 1 + 3 x 2 = 2 x
A. 0 B. 1
C. 2 D. Vô số