Các câu hỏi tương tự
Trong mặt phẳng tọa độ Oxy, biết điểm M’(-3;0) là ảnh của điểm M(1;-2) qua phép tịnh tiến theo vectơ
u
→
và M”(2;3) là ảnh của điểm M’ qua phép tịnh tiến theo vectơ
v
→
. Tìm tọa độ vectơ
u
→
+
v
→
. A. (1;5) B. (-4;2) C. (5;3) D. (0;1)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, biết điểm M’(-3;0) là ảnh của điểm M(1;-2) qua phép tịnh tiến theo vectơ u → và M”(2;3) là ảnh của điểm M’ qua phép tịnh tiến theo vectơ v → . Tìm tọa độ vectơ u → + v → .
A. (1;5)
B. (-4;2)
C. (5;3)
D. (0;1)
Cho hai parabol
P
1
:
y
x
2
+
3
x
−
2
và
P
2
:
y
x
2
+
5
x
+
4
. Phép tịnh tiến theo
v
→
a
;...
Đọc tiếp
Cho hai parabol P 1 : y = x 2 + 3 x − 2 và P 2 : y = x 2 + 5 x + 4 . Phép tịnh tiến theo v → = a ; b biến P 1 thành P 2 thì a+b bằng
A. 3
B. -3
C. -1
D. 1
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
x
1
+
t
y
2
-
2
t
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 x = 1 + t y = 2 - 2 t z = - 3 - t và d 2 x = 4 + 3 t y = 3 + 2 t z = 1 - t . Trên đường thẳng d₁ lấy hai điểm A, B thỏa mã AB=3. Trên đường thẳng d₂ lấy hai điểm C, D thỏa mãn CD=4. Tính thể tích V của tứ diện ABCD.
A. V=7
B. V=2 21
C.V= 4 21 3
D.V= 5 21 6
Cho đường tròn (C)
x
-
2
2
+
y
-
4
2
1
. Đường thẳng d có phương trình 3x-4y0. Tính thể tích V của hình xuyến tạo thành khi quay đường tròn (C) quanh đường thẳng d. A.
π
2
B. ...
Đọc tiếp
Cho đường tròn (C) x - 2 2 + y - 4 2 = 1 . Đường thẳng d có phương trình 3x-4y=0. Tính thể tích V của hình xuyến tạo thành khi quay đường tròn (C) quanh đường thẳng d.
A. π 2
B. 2 π 2
C. 4 π .
D. 4 π 2
Có bao nhiêu phép tịnh tiến biến một đường thẳng thành chính nó?
A. Không có
B. 1
C. 2
D. Vô số
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:y −
x
3
+ 3x + 1b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàmsố:y
(
x
+
1
)
3
− 3x − 4c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình:
(
x
+
1...
Đọc tiếp
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:
y = − x 3 + 3x + 1
b) Chỉ ra phép biến hình biến (C) thành đồ thị (C’) của hàmsố:
y = ( x + 1 ) 3 − 3x − 4
c) Dựa vào đồ thị (C’), biện luận theo m số nghiệm của phương trình:
( x + 1 ) 3 = 3x + m
d) Viết phương trình tiếp tuyến (d) của đồ thị (C’), biết tiếp tuyến đó vuông góc với đường thẳng
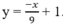
Trong không gian Oxyz, cho mặt phẳng
(
α
)
:
2
x
+
y
-
2
z
-
2
0
đường thẳng
d
:
x...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2 x + y - 2 z - 2 = 0 đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng ( α ) , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 3
B. 7 2
C. 21 2
D. 3 2
Trong không gian Oxyz, cho mặt phẳng (α): 2x+y-2z-20, đường thẳng
d
:
x
+
1
1
y
+
2
2
z
+
3
2
và điểm
A
(
1
2
;
1
;
1...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (α): 2x+y-2z-2=0, đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A ( 1 2 ; 1 ; 1 ) . Gọi Δ là đường thẳng nằm trong mặt phẳng (α), song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:
A. 7/2
B. 21 / 2
C. 7/3
D. 3/2
Trong không gian Oxyz, cho ba điểm A(1; 2; 0), B(-2; 1; 3), C(7; -3; -6). Viết phương trình tham số của đường thẳng d đi qua trọng tâm G của tam giác ABC, đồng thời d song song với hai mặt phẳng (Oxy) và (Oxz) A. x 2 + t, y 0, z -1 B. x -2 + t, y 0, z -1 C. x 1 + 2t, y 0, z -t D. x 6 + t, y 0, z -3
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(1; 2; 0), B(-2; 1; 3), C(7; -3; -6). Viết phương trình tham số của đường thẳng d đi qua trọng tâm G của tam giác ABC, đồng thời d song song với hai mặt phẳng (Oxy) và (Oxz)
A. x = 2 + t, y = 0, z = -1
B. x = -2 + t, y = 0, z = -1
C. x = 1 + 2t, y = 0, z = -t
D. x = 6 + t, y = 0, z = -3




