1.
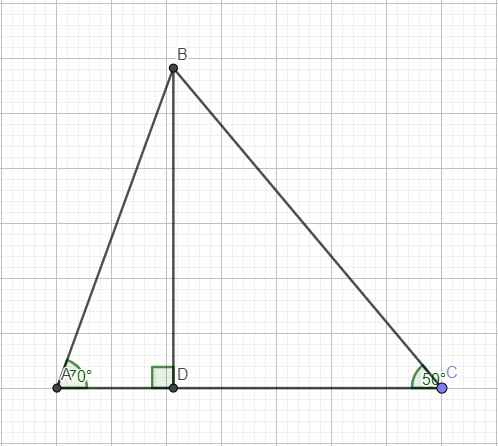
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)
2.
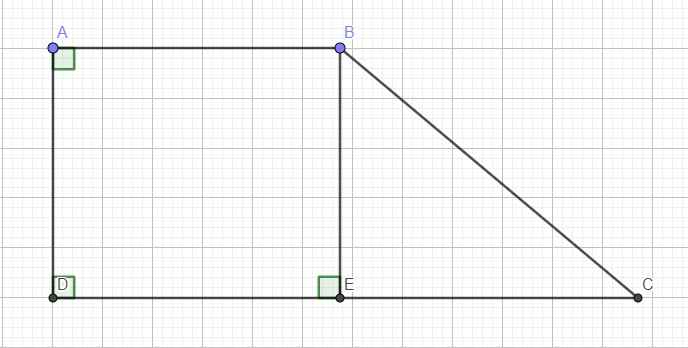
Ta có \(A+D=180^0\Rightarrow AB||CD\) (hai góc trong cùng phía bù nhau)
\(\Rightarrow\) Tứ giác ABCD là hình thang vuông tại A và D
Từ B kẻ BE vuông góc CD \(\Rightarrow ABED\) là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow\left\{{}\begin{matrix}DE=AB=4\left(cm\right)\\BE=AD=3\left(cm\right)\end{matrix}\right.\)
Trong tam giác vuông BCE:
\(tanC=\dfrac{BE}{CE}\Rightarrow CE=\dfrac{BE}{tanC}=\dfrac{3}{tan40^0}\approx3,6\left(cm\right)\)
\(\Rightarrow CD=DE+CE=4+3,6=7,6\left(cm\right)\)
\(\Rightarrow S_{ABCD}=\dfrac{1}{2}AD.\left(AB+CD\right)=\dfrac{1}{2}.3.\left(4+7,6\right)=17,4\left(cm^2\right)\)