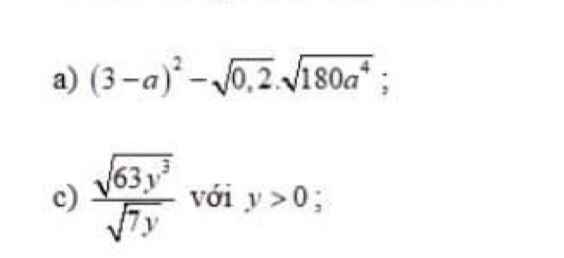Lời giải:
$\frac{1}{a}+\frac{1}{b}-\frac{1}{c}=\frac{1}{a+b-c}$
$\Leftrightarrow \frac{a+b}{ab}-(\frac{1}{c}+\frac{1}{a+b-c})=0$
$\Leftrightarrow \frac{a+b}{ab}-\frac{a+b}{c(a+b-c)}=0$
$\Leftrightarrow (a+b)(\frac{1}{ab}-\frac{1}{c(a+b-c)})=0$
$\Leftrightarrow (a+b).\frac{c(a+b-c)-ab}{abc(a+b-c)}=0$
$\Leftrightarrow (a+b).\frac{(a-c)(c-b)}{abc(a+b-c)}=0$
$\Leftrightarrow (a+b)(a-c)(c-b)=0$
$\Rightarrow a+b=0$ hoặc $a-c=0$ hoặc $c-b=0$
Nếu $a+b=0\Rightarrow a=-b$. Khi đó:
$\frac{1}{a^3}+\frac{1}{b^3}-\frac{1}{c^3}=\frac{1}{(-b)^3}+\frac{1}{b^3}-\frac{1}{c^3}=\frac{-1}{c^3}=\frac{1}{(-b)^3+b^3-c^3}=\frac{1}{a^3+b^3-c^3}$ (đpcm)
Tương tự với 2 TH $a-c=0$ và $c-b=0$
Do đó ta có đpcm.

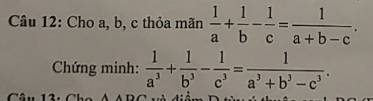



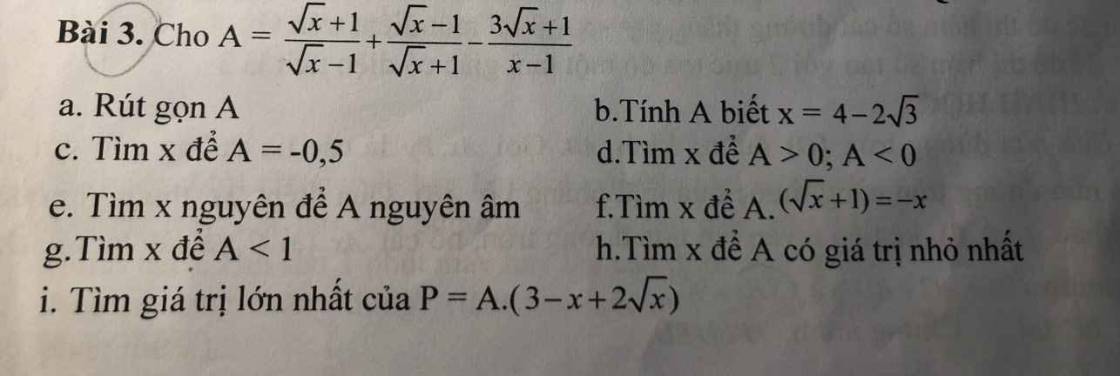 cíu cíu
cíu cíu cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui

 cíu lẹ cíu lẹ
cíu lẹ cíu lẹ