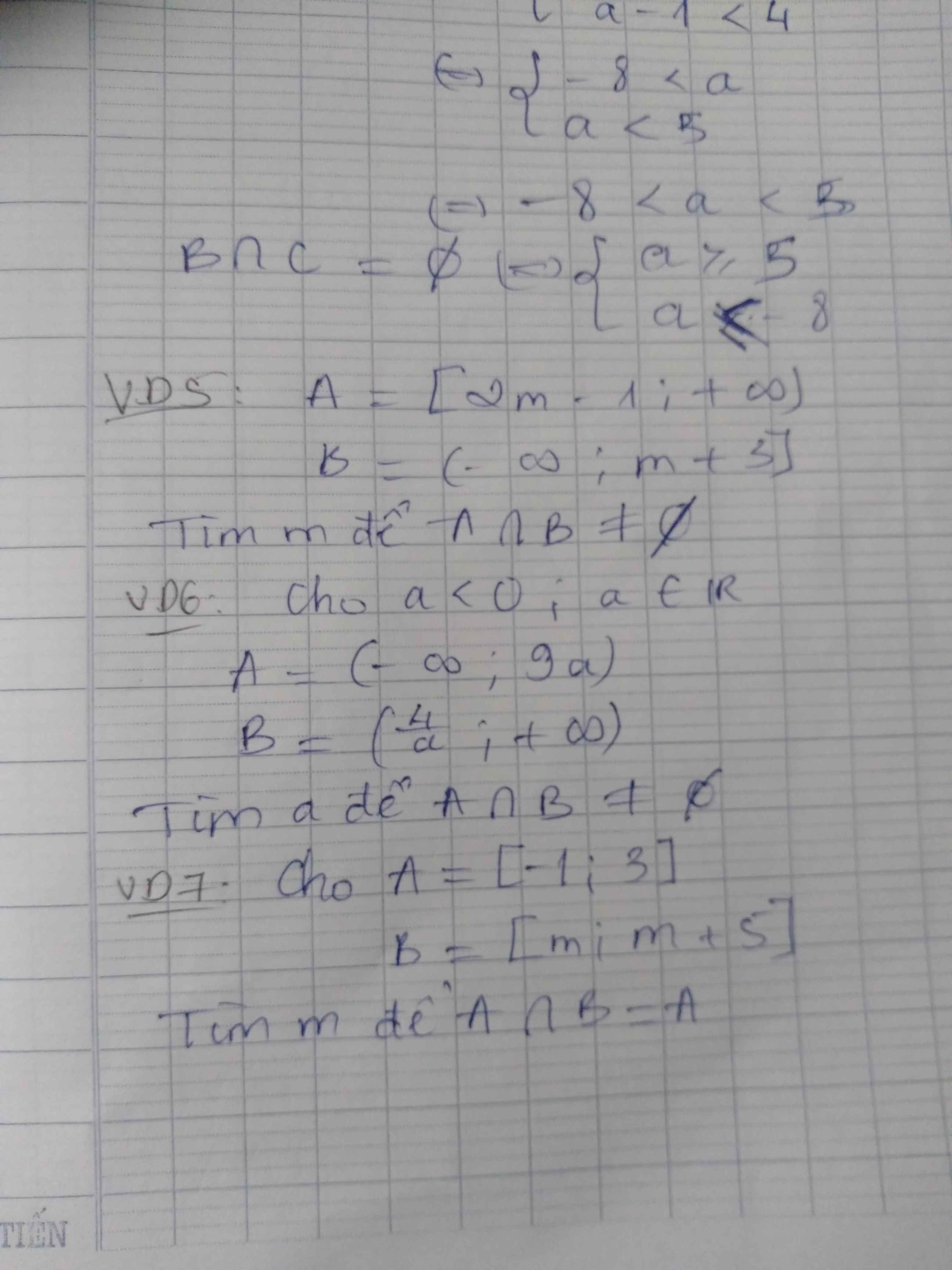cíu vs
Bài 15. Trong mặt phẳng tọa độ Oxy, cho ba điểm \( A(1;-1), B(-1;3), C(-2;0) \)
a) Chứng minh ba điểm \( A, B, C \) là ba đỉnh của một tam giác vuông cân tại \( C \).
b) Tính chu vi và diện tích của \( \triangle ABC \).
c) Tính \( \cos B \).
d) Tìm tọa độ tâm \( I \) và tính bán kính của đường tròn ngoại tiếp \( \triangle ABC \).
a: A(1;-1); B(-1;3); C(-2;0)
\(CA=\sqrt{\left(1+2\right)^2+\left(-1-0\right)^2}=\sqrt{3^2+1^2}=\sqrt{10}\)
\(CB=\sqrt{\left\lbrack-1-\left(-2\right)\right\rbrack^2+\left(3-0\right)^2}=\sqrt{\left(-1+2\right)^2+9}=\sqrt{10}\)
\(AB=\sqrt{\left(-1-1\right)^2+\left(3+1\right)^2}=\sqrt{\left(-2\right)^2+4^2}=2\sqrt5\)
Xét ΔCAB có \(CA^2+CB^2=AB^2\)
nên ΔCAB vuông tại C
mà CA=CB
nên ΔCAB vuông cân tại C
b: Chu vi tam giác CAB là:
\(CA+CB+AB=\sqrt{10}+\sqrt{10}+2\sqrt5=2\sqrt5+2\sqrt{10}\)
Diện tích tam giác CAB là:
\(S_{CAB}=\frac12\cdot CA\cdot CB=\frac12\cdot\sqrt{10}\cdot\sqrt{10}=\frac12\cdot10=5\)
c: ΔCAB vuông cân tại C
=>\(\hat{CBA}=45^0\)
=>\(cosCBA=\frac{\sqrt2}{2}\)
d: ΔCAB vuông tại C
mà I là tâm đường tròn ngoại tiếp
nên I là trung điểm của AB
Tọa độ điểm I là:
\(\begin{cases}x=\frac{1+\left(-1\right)}{2}=-\frac02=0\\ y=\frac{-1+3}{2}=\frac22=1\end{cases}\)
=>I(0;1)
Bán kính là \(\frac{AB}{2}=\sqrt5\)





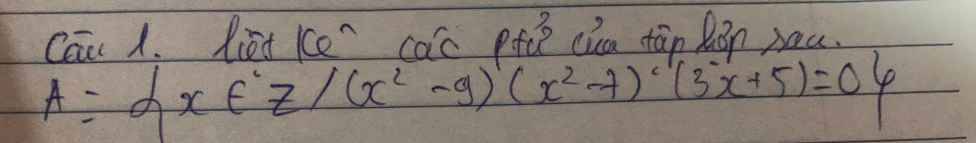 cíu bé vs mn ơi
cíu bé vs mn ơi

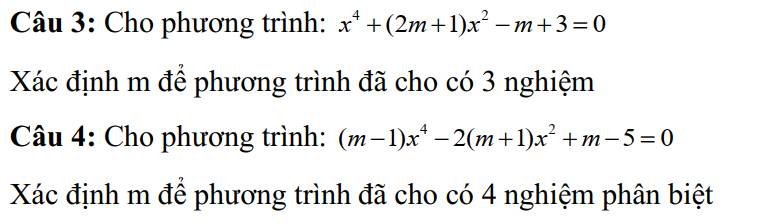 CÍU TUIIII
CÍU TUIIII