a. Em tự giải
b.
\(B=\dfrac{3\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-4\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}+\dfrac{x+6}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\left(\sqrt{x}-2\right)+\sqrt{x}\left(\sqrt{x}-4\right)+x+6}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2x-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}\left(2\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}-2}\)
c.
\(A< B\Rightarrow\dfrac{x}{\sqrt{x}-2}< \dfrac{2\sqrt{x}-1}{\sqrt{x}-2}\)
\(\Leftrightarrow\dfrac{x}{\sqrt{x}-2}-\dfrac{2\sqrt{x}-1}{\sqrt{x}-2}< 0\)
\(\Leftrightarrow\dfrac{x-2\sqrt{x}+1}{\sqrt{x}-2}< 0\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-2}< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}-1\ne0\\\sqrt{x}-2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}\ne1\\\sqrt{x}< 2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x< 4\end{matrix}\right.\)
Kết hợp ĐKXĐ \(\Rightarrow\left\{{}\begin{matrix}0< x< 4\\x\ne1\end{matrix}\right.\)

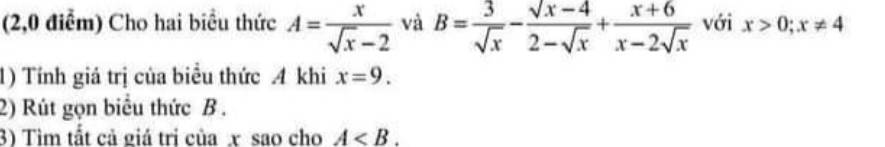



 cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui



 cíu cíu
cíu cíu cíu lẹ cíu lẹ
cíu lẹ cíu lẹ