a:
Sửa đề: (d): y=2(m+1)x-4m
Phương trình hoành độ giao điểm là:
\(x^2=2\left(m+1\right)x-4m\)
=>\(x^2-\left(2m+2\right)x+4m=0\)(1)
\(\Delta=\left(2m+2\right)^2-4\cdot1\cdot4m\)
\(=4m^2+8m+4-16m=4m^2-8m+4=\left(2m-2\right)^2\)
Để (P) tiếp xúc với (d) thì \(\Delta=0\)
=>2m-2=0
=>m=1
Thay m=1 vào (1), ta được:
\(x^2-\left(2\cdot1+2\right)x+4\cdot1=0\)
=>\(x^2-4x+4=0\)
=>(x-2)^2=0
=>x-2=0
=>x=2
=>\(y=2^2=4\)
vậy: Tọa độ tiếp điểm là A(2;4)
b: Để (d) cắt (P) tại hai điểm phân biệt thì \(\Delta>0\)
=>\(\left(2m-2\right)^2>0\)
=>\(2m-2\ne0\)
=>\(m\ne1\)
Khi m<>1 thì phương trình (1) sẽ có hai nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{2m+2-\left(2m-2\right)}{2}=\dfrac{2m+2-2m+2}{2}=2\\x=\dfrac{2m+2+\left(2m-2\right)}{2}=\dfrac{4m}{2}=2m\end{matrix}\right.\)
\(x_1^3-x_2^3=4\)
=>\(\left[{}\begin{matrix}2^3-\left(2m\right)^3=4\\\left(2m\right)^3-2^3=4\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}8-8m^3=4\\8m^3=8+4=12\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m^3=\dfrac{1}{2}\\m^3=\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1}{\sqrt[3]{2}}\left(nhận\right)\\m=\sqrt[3]{\dfrac{3}{2}}\left(nhận\right)\end{matrix}\right.\)





 cíu tui cíu tui
cíu tui cíu tui cíu tui cíu tui
cíu tui cíu tui

 cíu tui cíu tui
cíu tui cíu tui

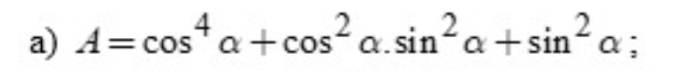
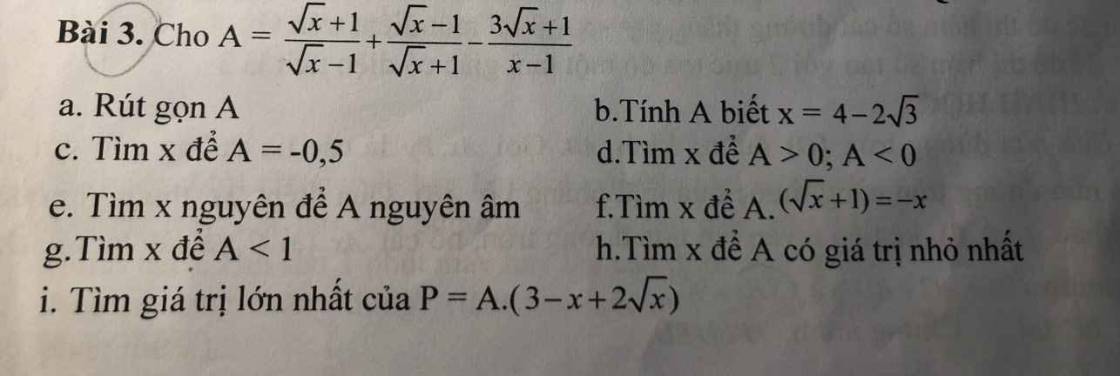 cíu cíu
cíu cíu cíu lẹ cíu lẹ
cíu lẹ cíu lẹ