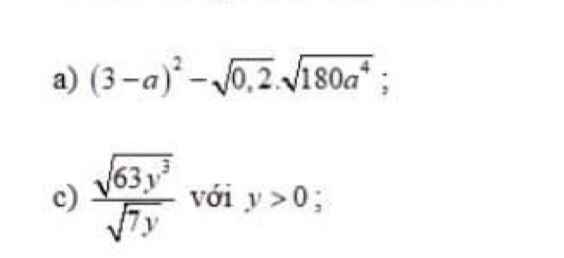Question

cíu cíu

Answer 1

a: Xét (O) có

\(\widehat{NDB}\) là góc tạo bởi tiếp tuyến DN và dây cung BD

\(\widehat{DAB}\) là góc nội tiếp chắn cung BD

Do đó: \(\widehat{NDB}=\widehat{DAB}\)

Xét ΔNDB và ΔNAD có

\(\widehat{NDB}=\widehat{NAD}\)

\(\widehat{DNB}\) chung

Do đó: ΔNDB~ΔNAD

=>\(\dfrac{ND}{NA}=\dfrac{NB}{ND}\)

=>\(ND^2=NA\cdot NB\)

b: Xét (O) có

\(\widehat{AID}\) là góc nội tiếp chắn cung AD

\(\widehat{ABD}\) là góc nội tiếp chắn cung AD

Do đó: \(\widehat{AID}=\widehat{ABD}\)

Xét ΔDIC và ΔABC có

\(\widehat{DIC}=\widehat{ABC}\)

\(\widehat{DCI}=\widehat{ACB}\)(hai góc đối đỉnh)

Do đó: ΔDIC~ΔABC