Các câu hỏi tương tự
Cho △ ABC nhọn nội tiếp đường tròn (O). Các đường cao AH,BK cắt nhau tại I. Kẻ đường kính AD.
a) Chứng minh △AIK đồng dạng △BIH
b)Chứng minh △AHC đồng dạng △BKC
c) chứng minh DC // BI
d) Chứng minh tứ giác BICD là hình bình hành
e) Kẻ OM⊥BC. Chứng minh OM=\(\dfrac{1}{2}\)AI
Từ một điểm A nằm ngoài (O;R) vẽ 2 tiếp tuyến Á và AJ a) chứng minh ẠO nội tiếp b) Vẽ cát tuyến ADE, chứng minh AD.AE = AS.AS c) Gọi H là trung điểm SJ, chứng minh: O;A;H thẳng hàng d) Chứng minh: AD.AE = AH.AO e) Chứng minh DHOE nội tiếp
Bài 1. Cho DDEF có ba góc nhọn nội tiếp (O), các đường cao DK, EH, FC cắt nhau tại I.a) Chứng minh các tứ giác DCIH, ECHF nội tiếpb) Chứng minh : DC.DE DH.DFc) Gọi giao điểm của CH với DI là G. Chứng minh và d) Chứng minh : DO ^ CH.e) Gọi A là trung điểm của EF, đường thẳng IA cắt cung nhỏ EF tại B. Chứng minh ba điểm D, O, B thẳng hàng.f) Tiếp tuyến tại E và F của đường tròn tâm O cắt nhau tại M. Chứng Minh ba điểm O, A, M thẳng hàng.
Đọc tiếp
Bài 1. Cho DDEF có ba góc nhọn nội tiếp (O), các đường cao DK, EH, FC cắt nhau tại I.
a) Chứng minh các tứ giác DCIH, ECHF nội tiếp
b) Chứng minh : DC.DE = DH.DF
c) Gọi giao điểm của CH với DI là G. Chứng minh và
d) Chứng minh : DO ^ CH.
e) Gọi A là trung điểm của EF, đường thẳng IA cắt cung nhỏ EF tại B. Chứng minh ba điểm D, O, B thẳng hàng.
f) Tiếp tuyến tại E và F của đường tròn tâm O cắt nhau tại M. Chứng Minh ba điểm O, A, M thẳng hàng.
Cho OM=3R. MA, MB là 2 tiếp tuyến. vẽ AD // MB. MD cắt đường tròn (O) tại C. BC cắt MA tại F. AC cắt MB tại E
a) Chứng minh: MAOB nội tiếp
b) Chứng minh: EB.EB = EC.EA
c) Chứng minh: E là trung điểm của MB
d) Chứng minh: BC.BM=MC.AB
e) Chứng minh: CF là tia phân giác của góc MCA
cho tam giác nhọn abc. các đường cao be, cf cắt nhau tại h . a) chứng minh ∆bhf ∽ ∆che b) chứng minh he.hb=hf. hc c) từ e hạ ei bc ( i thuộc bc). biết ec=15cm; ic= 9cm. chứng minh ∆bec ∽∆ eic. tính bc và be. d) chứng minh: bh.be+ch.cf= bc2
Cho tam giác ABC nhọn nội tiếp (O) vẽ 2 đường cao BM và CN cắt nhau tại H
a/ Chứng minh AH vuông góc BC
b/ Chứng minh tứ giác AMHN nội tiếp
c/ Chứng minh BCMN thuộc đường tròn xác định tâm I
d/ Vẽ tiếp tuyến Ax. Chứng minh OA vuông góc MN
Cho tam giác ABC vuông tại A, đường cao AH1) Tính AB, AC, AH khi HB 4 cm, HC9 cm.2) Gọi D, E lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng DE2 HB.HC3) Chứng minh rằng AE.ACAD.AB4) Chứng minh rằng BD.BA + AE.ACAB25) Chứng minh rằng Δ AED và Δ ABC đồng dạng6) Kẻ trung tuyến AM. Chứng minh rằng AM ⊥ DE
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH
1) Tính AB, AC, AH khi HB= 4 cm, HC=9 cm.
2) Gọi D, E lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng DE2 = HB.HC
3) Chứng minh rằng AE.AC=AD.AB
4) Chứng minh rằng BD.BA + AE.AC=AB2
5) Chứng minh rằng Δ AED và Δ ABC đồng dạng
6) Kẻ trung tuyến AM. Chứng minh rằng AM ⊥ DE
Cho OM=3R. MA, MB là 2 tiếp tuyến. vẽ AD // MB. MD cắt đường tròn (O) tại C. BC cắt MA tại F. AC cắt MB tại E[/size]
a) Chứng minh: MAOB nội tiếp[/size]
b) Chứng minh: EB.EB = EC.EA[/size]
c) Chứng minh: E là trung điểm của MB[/size]
d) Chứng minh: BC.BM=MC.AB[/size]
e) Chứng minh: CF là tia phân giác của góc MCA
Cho ΔABC , đường cao AH với H thuộc BC và ABAC . Gọi hình chiếu của H lên các đoạn thẳng AB AC , lần lượt là M và N.a) Chứng minh ΔAHM ~ ΔABH . Từ đó chứng minh AH^2 AM.AB .b) Chứng minh AM.ABAN.AC . Từ đó chứng minh ΔAMN~ΔACB .c) Giả sử ΔABC vuông tại A và AB6cm và AC8cm . Tính tỷ số diện tích của tứ giác BMNC và ΔABCd) Chứng minh 4 đường trung trực của các đoạn thẳng BM,MN,NC,CB đồng quy tại một điểm.tui còn mỗi câu c và d thôi ai giúp với
Đọc tiếp
Cho ΔABC , đường cao AH với H thuộc BC và AB<AC . Gọi hình chiếu của H lên các đoạn thẳng AB AC , lần lượt là M và N.
a) Chứng minh ΔAHM ~ ΔABH . Từ đó chứng minh AH^2= AM.AB .
b) Chứng minh AM.AB=AN.AC . Từ đó chứng minh ΔAMN~ΔACB .
c) Giả sử ΔABC vuông tại A và AB=6cm và AC=8cm . Tính tỷ số diện tích của tứ giác BMNC và ΔABC
d) Chứng minh 4 đường trung trực của các đoạn thẳng BM,MN,NC,CB đồng quy tại một điểm.
tui còn mỗi câu c và d thôi ai giúp với
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao BH, CK cắt nhau tại I. M là trung điểm của AH
a) Chứng minh A, H, I, K cùng thuộc một đường tròn
b) Vẽ đường kính AD, chứng minh tam giác ACD vuông từ đó chứng minh BH // CD
c) Chứng minh tứ giác BICD là hình bình hành.

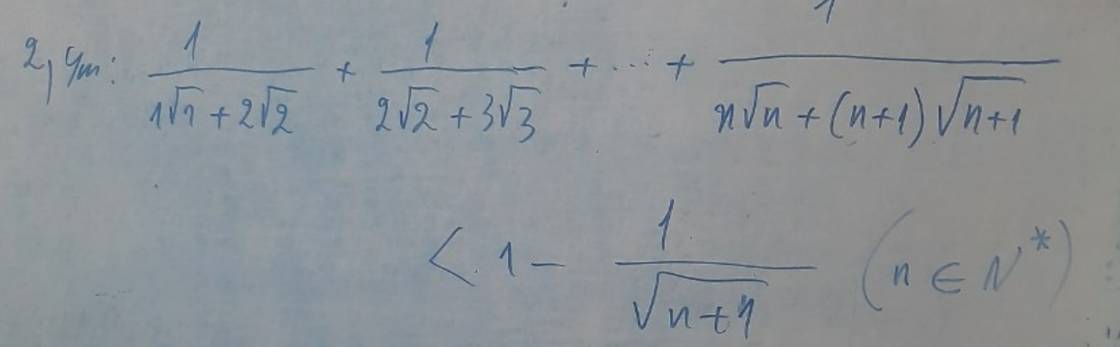 chứng minh
chứng minh 









