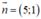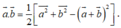a: ABCD là hình bình hành tâm O
=>O là trung điểm chung của AC và BD
Xét ΔABC có
AI,BO là đường trung tuyến
G là trọng tâm
Do đó: AI cắt BO tại G
\(2\cdot\overrightarrow{AO}+\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{AB}=2\cdot\overrightarrow{AI}\)
b: \(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{DB}+\overrightarrow{DB}\)
\(=2\cdot\overrightarrow{DB}\)
Xét ΔABC có
BO là đường trung tuyến
G là trọng tâm
Do đó: \(BG=\frac23BO\)
=>\(OG=\frac13BO=\frac13DO\)
=>\(DO=3\cdot OG\)
=>DB=6OG
DG=DO+OG=3OG+OG=4OG
=>\(DG=\frac23DB\)
=>\(DB=\frac32DG\)
=>\(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=2\cdot\overrightarrow{DB}=2\cdot\frac32\cdot\overrightarrow{DG}=3\cdot\overrightarrow{DG}\)
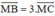
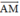
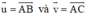
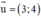và {\displaystyle {\vec {d}}}
đều khác 
Gọi 
là góc giữa hai vec tơ đó.
;
