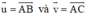1: \(\left|\overrightarrow{AB}-\overrightarrow{CB}+\overrightarrow{AC}\right|=\left|\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AC}\right|\)
\(=\left|\overrightarrow{AC}+\overrightarrow{AC}\right|=\left|2\cdot\overrightarrow{AC}\right|=2\cdot AC=2a\)
2: \(5\cdot\overrightarrow{AD}=2\cdot\overrightarrow{AC}\)
=>\(\overrightarrow{AD}=\frac25\cdot\overrightarrow{AC}\)
=>D nằm giữa A và C và AD=2/5AC
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+\frac12\cdot\overrightarrow{BD}=\overrightarrow{AB}+\frac12\left(\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\frac12\cdot\overrightarrow{AB}+\frac12\cdot\overrightarrow{AD}=\frac12\cdot\overrightarrow{AB}+\frac12\cdot\frac25\cdot\overrightarrow{AC}=\frac12\cdot\overrightarrow{AB}+\frac15\cdot\overrightarrow{AC}\)
\(\overrightarrow{AI}=\overrightarrow{AB}+\overrightarrow{BI}=\overrightarrow{AB}+x\cdot\overrightarrow{BC}\)
\(=\overrightarrow{AB}+x\left(\overrightarrow{BA}_{}+\overrightarrow{AC}\right)=\overrightarrow{AB}\left(1-x\right)+x\cdot\overrightarrow{AC}\)
Để A,M,I thẳng hàng thì \(\frac{1-x}{\frac12}=\frac{x}{\frac15}\)
=>2(1-x)=5x
=>5x=2-2x
=>7x=2
=>\(x=\frac27\)
;
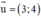và {\displaystyle {\vec {d}}}
đều khác 
Gọi 
là góc giữa hai vec tơ đó.
