Trong tam giác ABC ta luôn có:
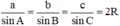 (Định lý Sin)
(Định lý Sin)
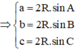
Trong tam giác ABC ta luôn có:
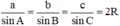 (Định lý Sin)
(Định lý Sin)
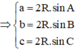
Cho tam giác ABC cân đỉnh A, ^A=α, AB=m, D là một điểm trên cạnh BC sao cho BC=3BD
a) Tính BC, AD
b) Chứng tỏ rằng đường tròn ngoại tiếp các tam giác ABD, ACD là bằng nhau. Tính cosα để bán kính chúng bằng 1/2 bán kính R của đường tròn ngoại tiếp tam giác ABC
Cho tam giác ABC có a,b,c,ma,mb,mc,R lần lượt là độ dài các cạnh BC,CA,AB, độ dài các đường trung tuyến kẻ từ A,B,C và bán kính đường tròn ngoại tiếp tam giác. Biết rằng: \(\frac{a^2+b^2}{mc}+\frac{b^2+c^2}{ma}+\frac{c^2+a^2}{mb}=12R\). Chứng minh rằng tam giác ABC đều
Cho tam giác ABC có AB = AC =2BC = a. Biết Rr =0,5 với R r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác ABC . Tính a
Cho tam giác ABC có a = 5, b = 12, c = 13. Bán kính đường tròn ngoại tiếp R của tam giác bằng
A. 13
B. 26
C. 6,5
D. 7,5
Cho tam giác ABC có a = 12, b = 16, c = 20. Tính diện tích S của tam giác, chiều cao ha, bán kính R, r của các đường tròn ngoại tiếp, nội tiếp tam giác và đường trung tuyến ma của tam giác
Cho tam giác ABC có b=45° và c=105° và phân giác trong của góc A là AD=4 bán kính đường tròn ngoại tiếp tam giác ABC là
CMR: tam giác ABC là đều khi và chỉ khi \(108Rr=7p^2+27r^2\) , trong đó p,R,r tương ứng là nửa chu vi, bán kính đường tròn ngoại tiếp và nội tiếp tam giác ABC.
cho 2 tam giác ABC và DEF có các góc đều nhọn và có: góc ABC=góc DEF ;góc BAC =góc EDF;AB=3.DE....chứng minh rằng bán kình đường trong ngoại tiếp tam giác ABC=3 lần bán kính đường trong ngoại tiếp tam giác DEF...
Tam giác ABC có BC =10 và A ^ = 30 O . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
A. R = 5
B. R = 10
C. R = 10 3
D. R = 10 3