Với a>b>0 để chứng minh a - b < a - b
ra quy về so sánh a v ớ i a - b + b
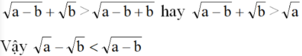
Với a>b>0 để chứng minh a - b < a - b
ra quy về so sánh a v ớ i a - b + b
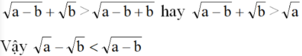
Chứng minh rằng, với a>b>0 thì a - b < a - b
a) So sánh .. 25 - 16 v à 25 - 16
b) Chứng minh rằng với a>b>0 thì
... a - b < a - b
chứng minh rằng,với hai số a,b thỏa mãn a>b>0 thì \(\sqrt{a}\)-\(\sqrt{b}\)<\(\sqrt{a-b}\)
chứng minh rằng,với hai số a,b thỏa mãn a>b>0 thì \(\sqrt{a}-\sqrt{b}\)<\(\sqrt{a-b}\)
a) Chứng minh rằng,với a>b>0 thì căn a-căn b<căn a-b
Chứng minh rằng : Với a > b > 0 thì \(\sqrt{a}-\sqrt{b}< \sqrt{a-b}\)
Chứng minh rằng với a+b>c và |a-b|<c với a,b,c >0 thì phương trình bậc hai a^2x^2 +(a^2+b^2-c^2)x +b^2=0 vô nghiệm
ĐOẠN MK BÔI ĐỎ GIẢI THÍCH HỘ
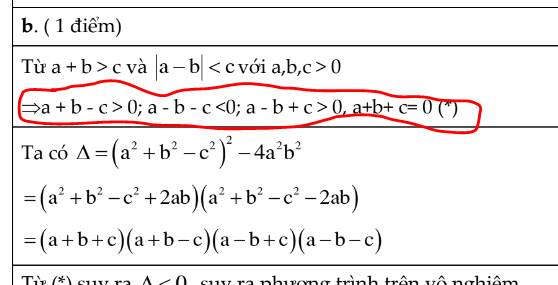
a) Chứng minh rằng với a, b , c là các số thực thì phương trình sau luôn có nghiệm:
(x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) = 0
b) Chứng minh rằng với ba số thức a, b , c phân biệt thì phương trình sau có hai nghiệm phân biết: 
c) Chứng minh rằng phương trình: c2x2 + (a2 – b2 – c2)x + b2 = 0 vô nghiệm với a, b, c là độ dài ba cạnh của một tam giác.
d) Chứng minh rằng phương trình bậc hai:
(a + b)2x2 – (a – b)(a2 – b2)x – 2ab(a2 + b2) = 0 luôn có hai nghiệm phân biệt.
chứng minh rằng với a>b>0 thì \(\sqrt{a}-\sqrt{b}>\sqrt{a-b}\)