Gọi ABCD là hình chữ nhật
M,N,P,Q là trung điểm 4 canh AB,BC,CD,DA
Kẻ đường chéo AC ,BD
Xét tam giác ABC,ta có M,N là đường trugn binh của tam giác ABC
=> MN //= 1/2 AC (1)
Chưng minh tương tự với tam giác ACD => PQ//= 1/2 AC (2)
Tam giac ABD có MQ là đường trung binh => MQ //=1/2 BD (3)
Tam giác BDC có NP là đương trung binh => NP //=1/2 BD (4)
tỪ (1),(2),(3),(4) có AC=BD (đương chéo chữ nhật)=>MN =NP=PQ=QM
Hay MNPQ là hinh thoi
chung minh rang cac trung diem cua 4 canh cua 1 hcn là các đỉnh cua hình thoi
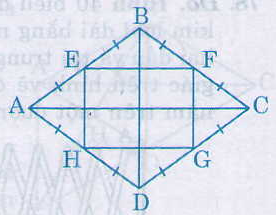
Ta có: EB = EA, FB = FA (gt)
nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
HD = HA, GD = GC (gt)
nên HG là đường trung bình của ∆ADC.
Do đó HG // AC
Suy ra EF // HG (1)
Chứng minh tương tự EH // FC (2)
Từ (1) (2) ta được EFGH là hình bình hành.
Lại có EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
nên = 900
Hình bình hành EFGH có = 900 nên là hình chữ nhật.
Gọi ABCD là hình chữ nhật
M,N,P,Q là trung điểm 4 canh AB,BC,CD,DA
Kẻ đường chéo AC ,BD
Xét tam giác ABC,ta có M,N là đường trugn binh của tam giác ABC
=> MN //= 1/2 AC (1)
Chưng minh tương tự với tam giác ACD => PQ//= 1/2 AC (2)
Tam giac ABD có MQ là đường trung binh => MQ //=1/2 BD (3)
Tam giác BDC có NP là đương trung binh => NP //=1/2 BD (4)
tỪ (1),(2),(3),(4) có AC=BD (đương chéo chữ nhật)=>MN =NP=PQ=QM
Hay MNPQ là hinh thoi










