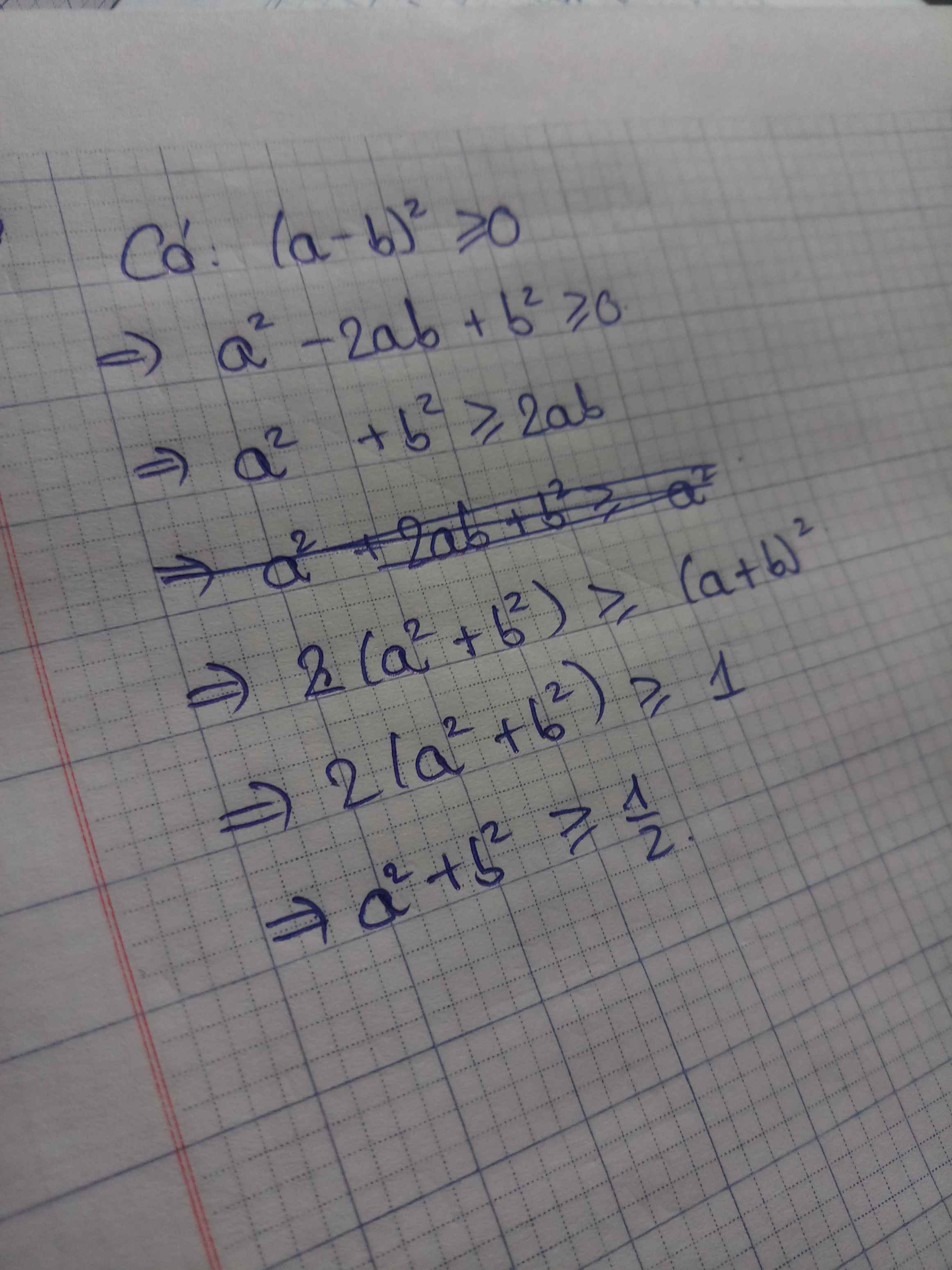Các câu hỏi tương tự
chứng minh rằng nếu:1/a+1/b+1/c=2 và a+b+c=a*b*c thì 1/a^2+1/b^2+1/c^2=3
Chứng minh rằng nếu a + b = 1 thì a2 + b2 ≥ 1/2
Chứng minh rằng nếu a + b = 1 thì a mũ 2 + b mũ 2 lớn hơn hoặc bằng 1 /2
Cho a^2+b^2+c^2+3= 2(a+b+c). Chứng minh a=b=c=1
2. Chứng minh rằng nếu a+b+c=0 thì a^3+b^3+c^3=3abc
Chứng minh rằng nếu a + b = 1 thì a2 + b2 >= 1/2
Chứng minh rằng nếu a,b,c \(\ge\)0 và abc=1 thì
\(\dfrac{1}{2+a}+\dfrac{1}{2+b}+\dfrac{1}{2+c}\le1\)
Chứng minh rằng nếu a + b = 1 t h ì a 2 + b 2 ≥ 1 / 2
Chứng minh rằng nếu a + b = 1 thì a2 + b2 ≥ 1/2
A, cho abc = 1 và a+b+c = 1/a +1/b +1/c. Chứng minh tồn tại một trong 3 số a,b,c bằng 1
B, chứng minh rằng nếu a + b + c = n và 1/a + 1/b + 1/c = 1/n thì tồn tại một trong ba số bằng n
C, chứng minh rằng nếu 3 số a,b,c khác 0 thì thỏa mãn đẳng thức
a2 -- b2 / ab + b2 -- c2 /bc + c2 -- a2/ca =0
thì tồn tại hai số bằng nhau