a)
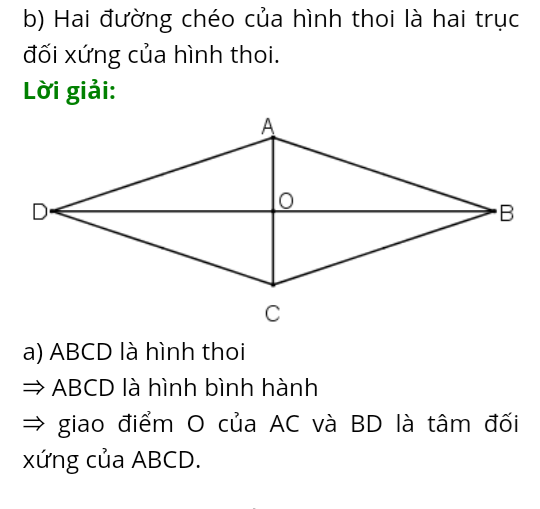
a) ABCD là hình thoi
=> ABCD là hình bình hành
=> giao điểm O của AC và BD là tâm đối xứng của ABCD
b)
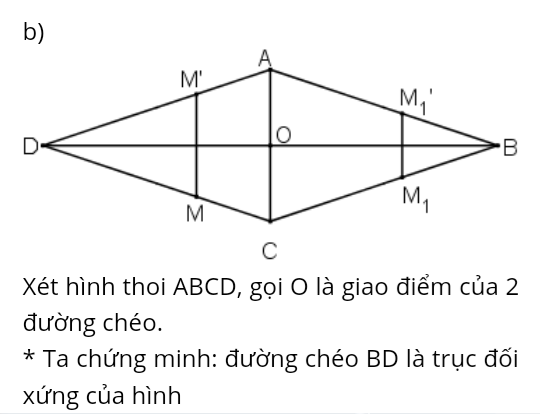
Xét hình thoi ABCD, gọi O là giao điểm của 2 đường chéo.
* Ta chứng minh: đường chéo BD là trục đối xứng của hình
Lấy điểm M bất kì thuộc hình thoi. Không mất tổng quát, M nằm trên CD.
Gọi M’ đối xứng với M qua đường thẳng BD. Ta chứng minh điểm M’ cũng thuộc hình thoi
+ Gọi I là giao điểm của MM’ và BD.
Xét tam giác DIM và DIM’ có :
\(\widehat{DIM}=\widehat{DIM'}=90^o\)
DI chung
IM= IM’ ( do M và M’ đối xứng với nhau qua BD)
\(=>\Delta DIM=\Delta DIM'\left(c.g.c\right)\)
=> DM = DM' và \(\widehat{IDM}=\widehat{IDM'}\left(1\right)\)
Ta lại có: ABCD là hình thoi nên
\(\widehat{IDA}=\widehat{IDC}\)hay \(\widehat{IDM}=\widehat{IDA}\left(2\right)\)
Từ (1) và (2) suy ra, điểm M’ nằm trên cạnh AD hay điểm M’ thuộc hình thoi
=> BD là trục đối xứng của hình thoi.
*Chứng minh tương tự, ta có: AC là trục đối xứng của hình thoi