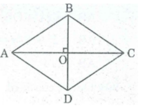
* Ta có: AC ⊥ BD (tính chất hình thoi)
OB = OD (tính chất hình thoi)
Nên AC là đường trung trực của BD.
Do đó điểm đối xứng với điểm B qua AC là D;
Điểm đối xứng với điểm D qua AC là B
Điểm đối xứng với điểm A qua AC là điểm A;
Điểm đối xứng với điểm C qua AC là điểm C
Vậy điểm đối xứng với mỗi đỉnh của hình thoi qua AC cũng thuộc hình thoi
Do đó AC là trục đối xứng của hình thoi ABCD.
* Ta có : OC = OA và AC ⊥ BD (tính chất hình thoi)
Nên BD là đường trung trực của AC
Do đó điểm đối xứng với điểm A qua BD là điểm C
Điểm đối xứng với điểm C qua BD là điểm A
Điểm đối xứng với điểm B qua BD là điểm B
Điểm đối xứng với điểm D qua BD là điểm D
Vậy điểm đối xứng với mỗi đỉnh của hình thoi qua BD cũng thuộc hình thoi.
Do đó BD là trục đối xứng của hình thoi ABCD.










