Xét a + b 8 với mọi a,b ≥ 0 ta có:
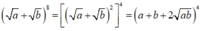
Áp dụng bất đẳng Cô-si cho hai số dương a + b và 2 a b ta được:
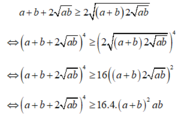
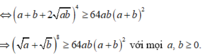
Xét a + b 8 với mọi a,b ≥ 0 ta có:
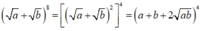
Áp dụng bất đẳng Cô-si cho hai số dương a + b và 2 a b ta được:
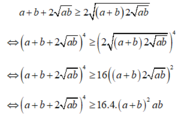
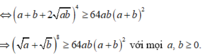
Giúp mình với mọi người, mình biết cách chứng minh rồi nhưng chưa hiểu lắm, mọi người làm lúc nào cũng được.
Chứng minh rằng: \(\frac{a^n+b^n+c^n}{3}\ge\left(\frac{a+b+c}{3}\right)^n,\forall a,b,c>0;n\in N\)
Trên Z xá định phép toán hai ngôi * như sau: với mọi a,b thuộc Z , a*b - a + b - 2. Chứng minh rằng Z cùng với phép toán * như trên lập thành một nhóm giao hoán
Cho 2 điểm phần biệt A, B. Xác định điểm M sao cho 2MA-3MB=0. Chứng minh rằng với mọi điểm Q ta luôn có 2QA-3QB=-QM ( vecto)
cho f(x)=x2 +ax+b. chứng minh rằng với mọi giá trị của a,b thì trong 3 số | f(0) |, | f(x) | , | f(-1)| có ít nhất 1 số lớn hơn hoặc bằng 1/2
$\rm Cho\ a,b,c \ge 0 .Thoả \ mãn \ ab+bc+ac=abc .Chứng \ minh\ a^{2}+b^{2}+c^{2}+5abc \ge 8$
`b)` Cho` a,b,c>=0,ab+bc+ca+abc=4`
CMR:`a^2+b^2+c^2+5abc>=8`
Chứng minh rằng a < b ⇔ a – b < 0.
Chứng minh rằng với mọi số thực a, b, c dương thỏa mãn a2 + b2 + c2 = 27. CMR:
\(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}=\frac{12}{a^2+63}+\frac{12}{b^2+63}+\frac{12}{c^2+63}\)
Cho a > 0, b > 0. Chứng minh rằng a b + b a ≥ a + b
\(a^4+b^4+ab\left(a+b\right)^2\ge2a^2b^2\)
CHỨNG MINH VỚI MỌI A,B thuộc R