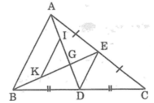
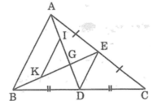
\(\text{Trên tia đối của NM lấy P sao cho NM=NP}\)
\(\text{Do MN là đường trung bình của }\Delta ABC\left(gt\right)\Rightarrow M\text{ là trung điểm AB, N là trung điểm AC}\)
\(\Rightarrow AM=BM\left(\text{do M là trung điểm AB}\right),AN=CN\left(\text{ do N là trung điểm AC}\right)\)
\(\Delta ANM=\Delta CNP\text{ do}\hept{\begin{cases}NM=NP\\\widehat{ANM}=\widehat{CNP}\left(\text{đối đỉnh}\right)\\AN=CN\left(cmt\right)\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\widehat{AMN}=\widehat{CPN}\left(2\text{ góc tương ứng}\right)\\AM=CP\left(2\text{ cạnh tương ứng}\right)\end{cases}}\)
\(\text{Do }\widehat{AMN}=\widehat{CPN}\left(cmt\right),\text{mà 2 góc này ở vị trí so le trong của 2 đường thẳng AB và NP}\Rightarrow\text{AB//NP}\)\(\left(\text{dấu hiệu nhận biết}\right)\)
\(\Rightarrow\text{BM//NP}\left(do\text{ M}\in AB\right)\Rightarrow\widehat{BMC}=\widehat{PCM}\left(2\text{ góc so le trong}\right)\)
\(\text{Vì AM=CP(cmt), mà AM=BM(gt)}\Rightarrow BM=CP\)
\(\Delta BMC=\Delta PCM\text{ do}\hept{\begin{cases}BM=CP\left(cmt\right)\\\widehat{BMC}=\widehat{PCM}\left(\text{cmt}\right)\\MC\text{ chung}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\widehat{BCM}=\widehat{PMC}\left(2\text{ góc tương ứng}\right)\\BC=PM\left(2\text{ cạnh tương ứng}\right)\end{cases}}\)
\(\text{Ta có:}\widehat{BCM}=\widehat{PMC}\left(cmt\right),\text{mà 2 góc này ở vị trí so le trong của 2 đường thẳng MN và BC}\Rightarrow\text{MN//BC}\left(1\right)\)
\(PM=2.MN\Rightarrow MN=\frac{PM}{2},\text{ mà PM=BC}\Rightarrow MN=\frac{BC}{2}\left(2\right)\)
\(\text{Từ (1) và (2)}\Rightarrow MN\text{// và =}\frac{1}{2}BC\left(đpcm\right)\)