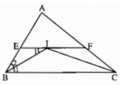
Gọi D là trung điểm của BC, E là trung điểm của AC. Theo câu a)) đường thẳng qua D, song song với AB phải cắt AC tại trung điểm của AC nên đường thẳng đó phải đi qua E, hay DE // AB.

Gọi D là trung điểm của BC, E là trung điểm của AC. Theo câu a)) đường thẳng qua D, song song với AB phải cắt AC tại trung điểm của AC nên đường thẳng đó phải đi qua E, hay DE // AB.
Cho tam giác ABC. Chứng minh rằng nếu một đường thẳng đi qua trung điểm của một cạnh và song song với cạnh thứ hai thì sẽ đi qua trung điểm cạnh thứ ba
qua mỗi đỉnh của tam giác kẻ đường song song với cạnh đối diện với nó a ) chứng minh rằng mỗi đường thẳng cắt hai đường thẳng còn lại b ) chứng minh rằng ba giao điểm là ba đỉnh của một tam giác .
Cho tam giác ABC. Chứng minh rằng: đương thẳng đi qua trung điểm 1 cạch và song song với cạnh thứ 2 thì đi qua trung điểm cạnh thứ 3
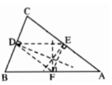
Cho tam giác ABC ,điểm D thuộc cạnh BC ,các đường thẳng đi qua D và song song với AC ,BA cắt AB, AC tại E và F . Gọi H và I là trung điểm của của BF và CE .
Chứng minh rằng :
a. Tam giác ACE =tam giác CBF
b. Chứng minh tam giác IDH đều
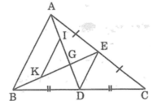
Theo kết quả của bài 64 chương II, sách Bài tập toán 7 tập một ta có: Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Vận dụng kết quả trên để giải bài toán sau: Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng:
AG = 2/3 AD
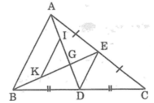
Theo kết quả của bài 64 chương II, sách Bài tập toán 7 tập một ta có: Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Vận dụng kết quả trên để giải bài toán sau: Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng:
IK // DE, IK = DE
a) Chứng minh rằng trong một tam giác, một góc sẽ là nhọn, vuông hay tù tùy theo cạnh đối diện với góc đó nhỏ hơn hay bằng hay lớn hơn hai lần đường trung tuyến kẻ tới cạnh đó
b) cho một tam giác có độ dài các cạnh là a,b,c đồng thời a-b=b-c. Điểm M là giao điểm của hai trung tuyến, P là giao điểm của các đường phân giác của góc trong tam giác đã cho. Chứng minh rằng MP song song với cạnh có độ dài bằng b
Bài 1. Cho tam giác ABC vuông tại A có góc B= 53 độ
a) Tính góc C.
b) Trên cạnh BC, lấy một điểm D sao cho BD=BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh tam giác BEA = tam giác BED.
Bài 2. Cho tam giác ABC có AB= AC và M là trung điểm của cạnh BC.
a) Chứng minh tam giác AMB = tam giác AMC.
b) Qua A, vẽ đường thẳng a vuông góc với AM. Chứng minh AM vuông góc với BC và a song song với BC.
c) Qua C, vẽ đường thẳng b song song với AM. Gọi N là giao điểm của hai đường thẳng a và b. Chứng minh tam giác AMC = tam giác CNA.
Bài 3. Cho tam giác ABC, gọi M là trung điểm của cạnh BC. Trên tia đối của tia MAlấy điểm D sao cho MD = MA.
a) Chứng minh tam giác MAB = tam giác MDC.
b) Chứng minh rằng AB = CD và AB // CD.
Bài 4. Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BE = BA. Vẽ AH vuông góc với BC tại H.
a) Chứng minh rằng: tam giác ABD = tam giác EBD và AD = ED.
b) Chứng minh rằng: AH // DE.
*Vẽ hình giúp mình*
Cho tam giác ABC. Gọi I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Qua I kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại E và F. Chứng minh rằng EF = BE + CF.