Question

Cho tam giác ABC. Gọi I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Qua I kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại E và F. Chứng minh rằng EF = BE + CF.

Answer 1

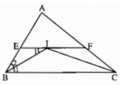
Vì điểm I cách đều ba cạnh của tam giác ABC và nằm trong tam giác nên I là giao điểm của ba đường phân giác của tam giác ABC, tức là BI, CI lần lượt là tia phân giác của góc N và góc C. Do EF // BC nên ∠B1= ∠I1(so le trong), suy ra ∠I2 = ∠B2 .

Suy ra: BI, CI lần lượt là tia phân giác của góc B và góc C.

Do EF // BC nên ∠B1 = ∠BIE (so le trong).

Lại có: ∠B1 = ∠B2 ( vì BI là tia phân giác của góc B )

Suy ra: ∠B2 = ∠BIE

Vậy EF = EI + IF = BE + CF.