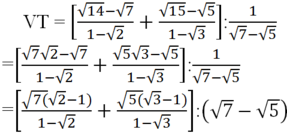
= (-√7 - √5)(√7 - √5)
= -(√7 + √5)(√7 - √5)
= -(7 - 5) = -2 = VP (đpcm)
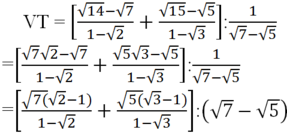
= (-√7 - √5)(√7 - √5)
= -(√7 + √5)(√7 - √5)
= -(7 - 5) = -2 = VP (đpcm)
chứng minh đẳng thức: \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)= -2
1.chứng minh các đẳng thức sau:
a.\(\frac{3}{2}\sqrt{6}+2\sqrt{\frac{2}{3}}-4\sqrt{\frac{3}{2}}=\frac{\sqrt{6}}{6}\)
b.\(\left(\frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\frac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\frac{1}{\sqrt{7}-\sqrt{5}}=-2\)
chứng minh các đẳng thức sau
a) \(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}=1\)
b) \(\sqrt[3]{20+14\sqrt{2}}-\sqrt[3]{14\sqrt{2}-20}=4\)
\(\sqrt[3]{5\sqrt{2}+7}-\sqrt[3]{5\sqrt{2}-7}=2\)
Chứng minh các đẳng thức sau:
a ) 2 3 − 6 8 − 2 − 216 3 ⋅ 1 6 = − 1 , 5 b ) 14 − 7 1 − 2 + 15 − 5 1 − 3 : 1 7 − 5 = − 2 c ) a b + b a a b : 1 a − b = a − b v ó i a , b d ư ơ n g v à a ≠ b . d ) 1 + a + a a + 1 ⋅ 1 − a − a a − 1 = 1 − a v ó i a ≥ 0 v à a ≠ 1
Chứng minh bất đẳng thức
a)√6-√2>1
b)√5-√3>1/2
c)√7-√6<√6-√5
d)√7-√2>1
Chứng minh các bất đẳng thức:
a) căn 6 - căn 2 >1
b) căn 5 - căn 3>1/2
c) căn 7 - căn 6 < căn 6 - căn 5
Với n là số tự nhiên, chứng minh đẳng thức:
n + 1 2 + n 2 = n + 1 2 - n 2
Viết đẳng thức trên khi n là 1, 2, 3, 4, 5, 6, 7
Chứng minh đẳng thức
\(\left(4-\sqrt{7}\right)^2=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}=-1,5\)
Chứng minh đẳng thức
\(\left(4-\sqrt{7}\right)^2=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}=-1,5\)