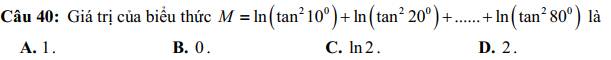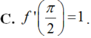Câu 31:
\(E=log_{\sqrt{5}}\left(\dfrac{a^3b^2}{\sqrt{c}}\right)\)
\(=\log_{5^{\dfrac{1}{2}}}\left(\dfrac{a^3b^2}{c^{\dfrac{1}{2}}}\right)\)
\(=2\cdot\log_5\left(\dfrac{a^3b^2}{c^{\dfrac{1}{2}}}\right)\)
\(=2\cdot log_5a^3+2\cdot log_5b^2-2\cdot log_5c^{\dfrac{1}{2}}\)
\(=6\cdot log_5a+4\cdot log_5b-log_5c\)
=6x+4y-z
=>Chọn C
Câu 40:
\(M=ln\left(tan^210^0\right)+ln\left(tan^220^0\right)+...+ln\left(tan^280^0\right)\)
\(=ln\left(tan^210^0\cdot tan^280^0\cdot tan^220^0\cdot tan^270^0\cdot tan^230^0\cdot tan^260^0\cdot tan^240^0\cdot tan^250^0\right)\)
\(=ln\left(1\cdot1\cdot1\cdot1\right)=ln1=0\)
=>Chọn B
Câu 32:
\(log_2a=3;log_2b=7\)
=>\(a=2^3;b=2^7\)
\(F=log_{ab}\left(\dfrac{a^2}{b}\right)\)
\(=log_{2^3\cdot2^7}\left(\dfrac{2^6}{2^7}\right)\)
\(=log_{2^{10}}\left(\dfrac{1}{2}\right)\)
\(=\dfrac{1}{10}\cdot log_2\left(2^{-1}\right)=\dfrac{1}{10}\cdot\left(-1\right)=-\dfrac{1}{10}\)
=>Chọn A
. Chọn đáp án sai:
