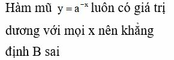Các câu hỏi tương tự
Cho 2 hàm số
y
f
x
log
a
x
;
y
g
x
a
x
.
Xét các mệnh đề sau:I. Đồ thị của hai hàm số
f
x
,
g
x
luôn cắt nhau tại một điểmII. Hàm số
f
x
+
g
x
đ...
Đọc tiếp
Cho 2 hàm số y = f x = log a x ; y = g x = a x . Xét các mệnh đề sau:
I. Đồ thị của hai hàm số f x , g x luôn cắt nhau tại một điểm
II. Hàm số f x + g x đồng biến khi a > 1 , nghịch biến khi 0 < a < 1
III. Đồ thị hàm số f x nhận trục Oy làm tiệm cận
IV. Chỉ có đồ thị hàm số f x có tiệm cận
Số mệnh đề đúng là
A. 1
B. 4
C. 2
D. 3
Xét các khẳng định sau:(I). Nếu hàm số y f(x) có giá trị cực đại là M và giá trị cực tiểu là m thì M m (II). Đồ thị hàm số
y
a
x
4
+
b
x
2
+
c
(
a
≠
0...
Đọc tiếp
Xét các khẳng định sau:
(I). Nếu hàm số y = f(x) có giá trị cực đại là M và giá trị cực tiểu là m thì M > m
(II). Đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III). Tiếp tuyến (nếu có) tại một điểm cực trị của đồ thị hàm số luôn song song với trục hoành.
Số khẳng định đúng là :
A. 0
B. 3
C. 2
D. 1
Cho hàm số yf(x) có đạo hàm liên tục trên R và có đồ thị yf(x) như hình vẽ bên. Đặt
g
(
x
)
f
(
x
)
-
x
2
2
biết rằngđồ thị của hàm g(x) luôn cắt trục hoành tại 4 điểm phân biệt. Mệnh đề nào dưới đây đúng A.
g
(...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có
đồ thị y=f'(x) như hình vẽ bên. Đặt g ( x ) = f ( x ) - x 2 2 biết rằng
đồ thị của hàm g(x) luôn cắt trục hoành tại 4 điểm phân biệt.
Mệnh đề nào dưới đây đúng

A. g ( 0 ) > 0 g ( 1 ) < 0 g ( - 2 ) g ( 1 ) > 0
B. g ( 0 ) > 0 g ( 1 ) > 0 g ( - 2 ) g ( 1 ) < 0
C. g ( 1 ) < 0 g ( 0 ) > 0
D. g ( 0 ) > 0 g ( - 2 ) < 0
Cho hàm số yf(x) xác định trên R. Đồ thị hàm số
y
f
(
x
)
cắt trục hoành tại 3 điểm a, b, c (
a
b
c
) như hình dưới: Biết f(b) 0 Đồ thị hàm số yf(x) cắt trục hoành tại bao nhiêu điểm phân biệt. A. 4 B. 1 C. 0 D. 2
Đọc tiếp
Cho hàm số y=f(x) xác định trên R. Đồ thị hàm số y = f ' ( x ) cắt trục hoành tại 3 điểm a, b, c ( a < b < c ) như hình dưới:
Biết f(b) < 0 Đồ thị hàm số y=f(x) cắt trục hoành tại bao nhiêu điểm phân biệt.
A. 4
B. 1
C. 0
D. 2
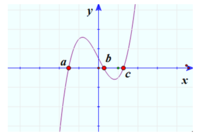
Cho đồ thị hàm số
y
e
−
x
2
như hình vẽ, ABCD là hình chữ nhật thay đổi sao cho B,C luôn thuộc đồ thị hàm số đã cho và A,D nằm trên trục hoành. Giá trị lớn nhất của diện tích hình chữ nhật ABCD A.
2
e
B. 2/e C.
2
e
D. ...
Đọc tiếp
Cho đồ thị hàm số y = e − x 2 như hình vẽ, ABCD là hình chữ nhật thay đổi sao cho B,C luôn thuộc đồ thị hàm số đã cho và A,D nằm trên trục hoành. Giá trị lớn nhất của diện tích hình chữ nhật ABCD
A. 2 e
B. 2/e
C. 2 e
D. 2 e
Cho hàm số
y
x
+
1
x
−
2
Số các giá trị tham số m để đường thẳng
y
m
+
x
luôn cắt đồ thị hàm số tại hai điểm phân biệt A, B sao cho trọng tâm tam giác OAB nằm trên đường tròn
x
2
+
y
2
−
3...
Đọc tiếp
Cho hàm số y = x + 1 x − 2 Số các giá trị tham số m để đường thẳng y = m + x luôn cắt đồ thị hàm số tại hai điểm phân biệt A, B sao cho trọng tâm tam giác OAB nằm trên đường tròn x 2 + y 2 − 3 y = 4 là
A. 1
B. 0
C. 3
D. 2
Cho hàm số
y
x
+
2
2
x
+
1
.
Xác định m để đường thẳng ymx+m-1 luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc hai nhánh của đồ thị A.m1 B.m0 C.m0 D.m0
Đọc tiếp
Cho hàm số y = x + 2 2 x + 1 . Xác định m để đường thẳng y=mx+m-1 luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc hai nhánh của đồ thị
A.m<1
B.m>0
C.m<0
D.m=0
Cho hàm số
y
f
x
có đạo hàm liên tục trên R và có đồ thị
y
f
x
như hình vẽ bên. Đặt
g
x
f
x
-
x
2
2
biết rằng đồ thị của hàm
g
x
luôn cắt trục hoành tại 4 điểm phân biệt. Mệnh đề nào dưới đây đúng...
Đọc tiếp
Cho hàm số y = f x có đạo hàm liên tục trên R và có đồ thị y = f ' x như hình vẽ bên.
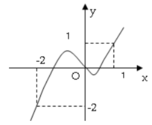
Đặt g x = f x - x 2 2 biết rằng đồ thị của hàm g x luôn cắt trục hoành tại 4 điểm phân biệt. Mệnh đề nào dưới đây đúng?
A. g 0 > 0 g 1 < 0 g - 2 g 1 > 0
B. g 0 > 0 g 1 > 0 g - 2 g 1 < 0
C. g ( 0 ) > 0 g ( 1 ) < 0
D. g ( 0 ) > 0 g ( - 2 ) < 0
Cho a là một số thực dương khác 1. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau: 1. Hàm số y
l
o
g
a
x
có tập xác định là D
(
0
;
+
∞
)
.
2. Hàm số y
l
o
g
a
x
là hàm đơn điệu trên khoảng
(
0
;
+
∞
)
.
3. Đồ thị hàm số y
l
o...
Đọc tiếp
Cho a là một số thực dương khác 1. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau:
1. Hàm số y= l o g a x có tập xác định là D= ( 0 ; + ∞ ) .
2. Hàm số y= l o g a x là hàm đơn điệu trên khoảng ( 0 ; + ∞ ) .
3. Đồ thị hàm số y= l o g a x và đồ thị hàm số y = a x đối xứng nhau qua đường thẳng y= x.
4. Đồ thị hàm số y= l o g a x nhận Ox là một tiệm cận
A. 4
B. 1
C. 3
D. 2
Biết hàm số yf(x) có đồ thị đối xứng với đồ thị hàm số
y
3
x
qua đường thẳng x-1. Chọn khẳng định đúng trong các khẳng định sau? A.
f
(
x
)
1
3
.
3
x
B.
f
(
x
)...
Đọc tiếp
Biết hàm số y=f(x) có đồ thị đối xứng với đồ thị hàm số y = 3 x qua đường thẳng x=-1. Chọn khẳng định đúng trong các khẳng định sau?
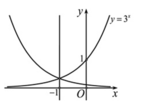
A. f ( x ) = 1 3 . 3 x
B. f ( x ) = 1 9 . 3 x
C. f ( x ) = 1 3 x - 1 2
D. f ( x ) = - 2 + 1 3 x