Các câu hỏi tương tự
Chọn hệ tọa độ Oxy sao cho trục Ox trùng với trục đối xứng, rồi dùng biểu thức tọa độ của phép đối xứng qua trục Ox để chứng minh tính chất 1.
Trong mặt phẳng với hệ tọa độ Oxy, tìm tọa độ điểm M’ là ảnh của điểm M(2 ; 1) qua phép đối xứng tâm I(3 ;-2).
A. M'(1;-3)
B. M'(-5;4)
C. M'(4;-5)
D. M'(1;5)
Trong mặt phẳng tọa độ Oxy phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k = 1/2 và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ.
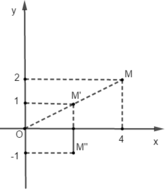
A.(2;-1)
B. (8;1)
C.(4;-2)
D. (8;4)
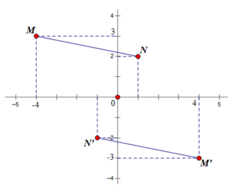
Trong mặt phẳng tọa độ Oxy cho điểm A(- 4;3). Tìm ảnh của A qua phép đối xứng tâm O.
Trong mặt phẳng tọa độ Oxy cho điểm A(-1;2) và đường thẳng d có phương trình
3
x
+
y
+
1
0
. Tìm ảnh của A và d.a. Qua phép tịnh tiến theo vectơ v(2;1);b. Qua phép đối xứng trục Oy;c. Qua phép đối xứng qua gốc tọa độ;d. Qua phép quay tâm O góc
90
o
.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho điểm A(-1;2) và đường thẳng d có phương trình 3 x + y + 1 = 0 . Tìm ảnh của A và d.
a. Qua phép tịnh tiến theo vectơ v=(2;1);
b. Qua phép đối xứng trục Oy;
c. Qua phép đối xứng qua gốc tọa độ;
d. Qua phép quay tâm O góc 90 o .
Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k
1
2
và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ: A. (2;-1) B. (8;1) C. (4;-2) D. (8;4)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O(0;0) tỉ số k= 1 2 và phép đối xứng trục Ox biến điểm M(4;2) thành điểm có tọa độ:
A. (2;-1)
B. (8;1)
C. (4;-2)
D. (8;4)
Trong mặt phẳng Oxy phép đối xứng tâm I biến M(6; -9) thành M'(3;7). Tọa độ của tâm đối xứng I là:
A. I(-3/2; -8)
B. (-3;16)
C. (9/2; -1)
D. I(-3/2; -1)
Trong mặt phẳng Oxy cho điểm M(-3;7). Phép đối xứng tâm O biến M thành M’ thì tọa độ M’ là:
A. M’(-3;-7)
B. M’(3;-7)
C. M’(7;-3)
D. M’(7;3)
Trong mặt phẳng Oxy, thực hiện liên tiếp phép quay tâm O góc quay - 45 o và phép đối xứng tâm O thì điểm M(1;1) biến thành điểm M’’ có tọa độ là:
A. (-1;0)
B. (√2;0)
C. (√2;-√2)
D. (-√2;0)