z 2 = a + bi 2 = a 2 - b 2 + 2abi
z 2 = a - b i 2 = a 2 - b 2 − 2abi
z. z = (a + bi)(a − bi) = a 2 + b 2
Từ đó suy ra các kết quả.
z 2 = a + bi 2 = a 2 - b 2 + 2abi
z 2 = a - b i 2 = a 2 - b 2 − 2abi
z. z = (a + bi)(a − bi) = a 2 + b 2
Từ đó suy ra các kết quả.
Cho z = a + bi . Chứng minh rằng:
a) z 2 + ( z ) 2 = 2( a 2 − b 2 )
b) z 2 − ( z ) 2 = 4abi
c) z 2 . = ( a 2 + b 2 ) 2
Cho số phức z = a + bi (với a,b là các số thực). Xét các phát biểu sau:
1:\(z^2-\overline{z}^2\) là số thực
2:\(z^2+\overline{z^2}\) là số ảo
3:\(z.\overline{z}\) là số thực
4:\(\left|z\right|-z\) bằng 0
Có bao nhiêu mệnh đề đúng?
A:0
B:1
C:2
D:3
Cho số phức z thỏa mãn z + 5 2 - 2 i = z + 3 2 + 2 i Biết biểu thức Q = z - 2 - 4 i + z - 4 - 6 i đặt giá trị nhỏ nhất tại z = a + b i a , b ∈ R Tính P = a - 4b
![]()
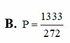
![]()
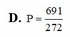
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(i+1) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho hai số phức z = - 2 + 5 i , z ' = a + b i ( a , b ∈ R ) Xác định a,b để z + z’ là một số thuần ảo
![]()
![]()
![]()
![]()
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Xét các số phức z = a + b i , ( a , b ∈ R ) thỏa mãn 4 ( z - z ¯ ) - 15 i = i ( z + z ¯ - 1 ) 2 . Tính F = - a + 4 b khi z - 1 2 + 3 i đạt giá trị nhỏ nhất
![]()
![]()
![]()
![]()
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa điều kiện (2-3i)z - 7i. z ¯ = 22-20i. Tính a+b
A. 3
B. -4
C. -6
D. 2
Cho số phức z = a + bi(a,b ∈ ℝ ) và xét hai số phức α = z 2 + ( z ¯ ) 2 v à β = 2 . z . z ¯ + i . ( z - z ¯ ) . Trong các khẳng định dưới đây, khẳng định nào đúng?
A. α là số thực, β là số thực.
B. α là số ảo, β là số thực.
C. α là số thực, β là số ảo.
D. α là số ảo, β là số ảo.