Câu 14. Cho biểu thức P x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.Câu 15. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:x2 + 4y2 + z2 – 2a + 8y – 6z + 15 0Câu 16. Tìm giá trị lớn nhất của biểu thức:Câu 17. So sánh các số thực sau (không dùng máy tính):Câu 18. Hãy viết một số hữu tỉ và một số vô tỉ lớn hơn √2 nhưng nhỏ hơn √3Câu 19. Giải phương trình: .Câu 20. Tìm giá trị lớn nhất của biểu thức A x2y với các điều kiện x, y 0 và 2x + x...
Đọc tiếp
Câu 14. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.
Câu 15. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:
x2 + 4y2 + z2 – 2a + 8y – 6z + 15 = 0
Câu 16. Tìm giá trị lớn nhất của biểu thức:
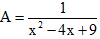
Câu 17. So sánh các số thực sau (không dùng máy tính):

Câu 18. Hãy viết một số hữu tỉ và một số vô tỉ lớn hơn √2 nhưng nhỏ hơn √3
Câu 19. Giải phương trình: 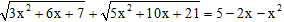 .
.
Câu 20. Tìm giá trị lớn nhất của biểu thức A = x2y với các điều kiện x, y > 0 và 2x + xy = 4.
Câu 21. Cho 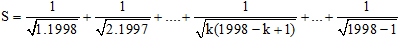 .
.
Hãy so sánh S và 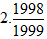 .
.
Câu 22. Chứng minh rằng: Nếu số tự nhiên a không phải là số chính phương thì √a là số vô tỉ.
Câu 23. Cho các số x và y cùng dấu. Chứng minh rằng:

Câu 24. Chứng minh rằng các số sau là số vô tỉ:

Câu 25. Có hai số vô tỉ dương nào mà tổng là số hữu tỉ không?
Câu 26. Cho các số x và y khác 0. Chứng minh rằng:
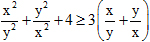
Câu 27. Cho các số x, y, z dương. Chứng minh rằng:
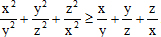
Câu 28. Chứng minh rằng tổng của một số hữu tỉ với một số vô tỉ là một số vô tỉ.
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.














