Các câu hỏi tương tự
Cho hai hàm số
f
(
x
)
x
2
và có
g
x
-
x
2
+
2
...
Đọc tiếp
Cho hai hàm số f ( x ) = x 2 và có g x = - x 2 + 2 n ế u x ≤ 1 2 n ế u - 1 < x < 1 - x 2 + 2 n ế u x ≥ 1 đồ thị như hình 55
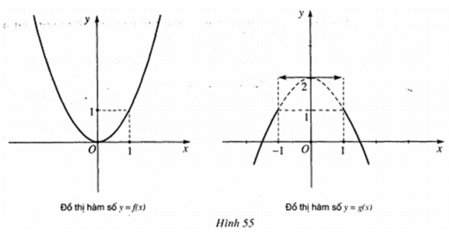
a) Tính giá trị của mỗi hàm số tại x = 1 và so sánh với giới hạn (nếu có) của hàm số đó khi x → 1 ;
b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ x = 1 .
Cho hai đường thẳng d: x + y - 1 = 0 và d’: x + y - 5 = 0. Phép tịnh tiến theo vecto u → biến đường thẳng d thành d’. khi đó, độ dài bé nhất của vecto u → là bao nhiêu?
A. 5
B. 4√2
C. 2√2
D. √2
cho đồ thị hàm số y=f(x),y=g(x) cùng tiếp xúc với đường thẳng (d):2x-y+1=0 tại M(1,3). Lập phương trình tiếp tuyến với đồ thị hàm số h(x)=f(x)*g(x)+2021x tại điểm có hoành độ bằng 1
Cho hàm số
f
x
3
x
+
2
n
ế
u
x
-
1...
Đọc tiếp
Cho hàm số f x = 3 x + 2 n ế u x < - 1 x 2 - 1 n ế u x ≥ - 1
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
Cho hai đường thẳng d: y x + y - 1 0 và d: x + y -5 0 Phép tịnh tiến theo vecto
u
→
biến đường thẳng d thành d Khi đó, độ dài bé nhất của
u
→
là bao nhiêu? A. 2
2
B. 5 C.
2
D. 4
2
Đọc tiếp
Cho hai đường thẳng d: y = x + y - 1 = 0 và d': x + y -5 = 0 Phép tịnh tiến theo vecto u → biến đường thẳng d thành d' Khi đó, độ dài bé nhất của u → là bao nhiêu?
A. 2 2
B. 5
C. 2
D. 4 2
Trong mặt phẳng tọa độ Oxy cho vectơ
v
→
-
1
;
2
,
A
3
;
5
,
B
-
1
;
1
và đường thẳng d có phương trình
x
–
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
Cho hàm số
y
f
(
x
)
có đồ thị
y
f
(
x
)
như hình vẽ bên. Đồ thị hàm số
g
(
x
)
2...
Đọc tiếp
Cho hàm số y = f ( x ) có đồ thị y = f ' ( x ) như hình vẽ bên. Đồ thị hàm số g ( x ) = 2 f ( x ) - ( x - 1 ) 2 có tối đa bao nhiêu điểm cực trị?
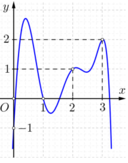
A. 3
B. 5
C. 6
D. 7
cho hàm số y=x^3+3x^2+1 có đồ thị (C)/.Gọi d là tiếp tuyến của C tại điểm A(1,5) và B la giao điểm thứ hai của d với C khi đó diện tích tam giác oab bằng
Cho hàm số y=f(x)=-x3+x2-1 có đồ thị (C):
Viết phương trình tiếp tuyến với đồ thị của hàm số tại điểm có hoành độ bằng 2