Các câu hỏi tương tự
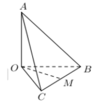
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau và OBOC Gọi M là trung điểm BC, OMa (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng OA và BC bằng A. a. B.
2
a
C.
2
a
2
D.
3...
Đọc tiếp
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau và OB=OC Gọi M là trung điểm BC, OM=a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng OA và BC bằng
A. a.
B. 2 a
C. 2 a 2
D. 3 a 2
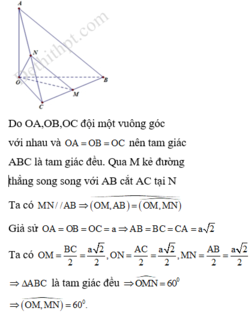
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và OAOBOC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng:
Đọc tiếp
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và OA=OB=OC. Gọi M là trung điểm của BC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng OM và AB bằng:
![]()
![]()
![]()
![]()
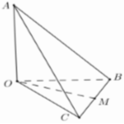
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và Gọi M là trung điểm BC (tham khảo hình vẽ bên). Góc giữa đường thẳng OM và AB bằng:
A
.
90
0
B
.
30
0
C
.
60
0
D
.
45
0
Đọc tiếp
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau và Gọi M là trung điểm BC (tham khảo hình vẽ bên). Góc giữa đường thẳng OM và AB bằng:
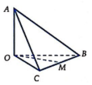
A . 90 0
B . 30 0
C . 60 0
D . 45 0
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc với nhau OA=OB=OC=a. Gọi M là trung điểm của BC. Khoảng cách giữa hai đường thẳng OM và AB bằng
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA OB OC. Khoảng cách giữa hai đường thẳng OA và BC bằng A.
a
2
B.
3
2
a
C.
3
2
2
a
D.
3
3
a...
Đọc tiếp
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = OB =OC. Khoảng cách giữa hai đường thẳng OA và BC bằng
A. a 2
B. 3 2 a
C. 3 2 2 a
D. 3 3 a 2
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA
a
2
2
, OB OC a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC) Tính thể tích khối tứ diện OABH A.
a
3
2
6
B.
a...
Đọc tiếp
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA = a 2 2 , OB= OC =a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC) Tính thể tích khối tứ diện OABH
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và đều có độ dài là l. Gọi M là trung điểm của các cạnh AB. Góc giữa hai vecto
O
M
→
và
B
C
→
bằng: A.
0
o
B.
45
o
C.
90
o
D.
120
o
Đọc tiếp
Tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và đều có độ dài là l. Gọi M là trung điểm của các cạnh AB. Góc giữa hai vecto O M → và B C → bằng:
A. 0 o
B. 45 o
C. 90 o
D. 120 o
Cho tứ diện OABC có OA,OB,OC đôi một tạo với nhau góc và OA OB a, OC 2a. Côsin góc giữa đường thẳng OC và mặt phẳng (ABC) bằng A.
5
3
B.
1
3
C.
2
3
D.
2...
Đọc tiếp
Cho tứ diện OABC có OA,OB,OC đôi một tạo với nhau góc và OA = OB= a, OC =2a. Côsin góc giữa đường thẳng OC và mặt phẳng (ABC) bằng
A. 5 3
B. 1 3
C. 2 3
D. 2 2 3
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc và các cạnh OA = OB = OC = a, gọi I là trung điểm BC.
a) Chứng minh rằng: BC ⊥ (AOI), (OAI) ⊥ (ABC).
b) Tính góc giữa AB và mặt phẳng (AOI).
c) Tính góc giữa các đường thẳng AI và OB.