Các câu hỏi tương tự
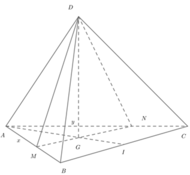
Cho tứ diện đều ABCD có cạnh bằng 1. M, N lần lượt là các điểm di động trên các cạnh AB, AC sao cho hai mặt phẳng (DMN), (ABC) vuông góc với nhau. Đặt
A
M
x
,
A
N
y
Đẳng thức nào sau đây đúng? A.
x
y
(
x
+
y
)
3
B. ...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 1. M, N lần lượt là các điểm di động trên các cạnh AB, AC sao cho hai mặt phẳng (DMN), (ABC) vuông góc với nhau. Đặt A M = x , A N = y Đẳng thức nào sau đây đúng?
A. x y ( x + y ) = 3
B. x + y = 3 x y
C. x + y = 3 + x y
D. x y = 3 ( x + y ) .
Cho tứ diện đều ABCD cạnh bằng 1. Xét các điểm M và N thay đổi lần lượt thuộc các cạnh AD, BC sao cho AMCNx (0x1). Gọi (P) là mặt phẳng chứa MN và song song với CD. Thiết diện của tứ diện với mặt phẳng (P) có diện tích nhỏ nhất bằng A.
1
4
B.
1
2
C.
3
4
D.
3
2
Đọc tiếp
Cho tứ diện đều ABCD cạnh bằng 1. Xét các điểm M và N thay đổi lần lượt thuộc các cạnh AD, BC sao cho AM=CN=x (0<x<1). Gọi (P) là mặt phẳng chứa MN và song song với CD. Thiết diện của tứ diện với mặt phẳng (P) có diện tích nhỏ nhất bằng
A. 1 4
B. 1 2
C. 3 4
D. 3 2
Cho tứ diện ABCD có AB vuông góc với CD, ABCD6. M là điểm thuộc canh BC sao cho MCx.BC (0x1). Mặt phẳng (P) đi qua M và song song với AB và CD lần lượt cắt BC, DB, AD, AC tại M, N, P, Q. Diện tích lớn nhất
S
m
a
x
của tứ giác MNPQ bằng bao nhiêu? A. 9 B. 4,5 C. 36 D. 18
Đọc tiếp
Cho tứ diện ABCD có AB vuông góc với CD, AB=CD=6. M là điểm thuộc canh BC sao cho MC=x.BC (0<x<1). Mặt phẳng (P) đi qua M và song song với AB và CD lần lượt cắt BC, DB, AD, AC tại M, N, P, Q. Diện tích lớn nhất S m a x của tứ giác MNPQ bằng bao nhiêu?
A. 9
B. 4,5
C. 36
D. 18
Trong không gian tọa độ Oxyz, cho đường thẳng
x
-
1
1
y
-
2
-
2
z
+
1
-
1
và mặt phẳng (P):2x - y - 2z - 2018 0. Phương trình mặt phẳng (Q) chứa đường thẳng D...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho đường thẳng x - 1 1 = y - 2 - 2 = z + 1 - 1 và mặt phẳng (P):2x - y - 2z - 2018 = 0. Phương trình mặt phẳng (Q) chứa đường thẳng D và tạo với (P) một góc nhỏ nhất cắt các trục tọa độ lần lượt tại các điểm A, B, C. Thể tích tứ diện O.ABC là:
A. 1 6
B. 32 3
C. 32 6
D. 64 3
Cho tứ diện ABCD có ABAC
2
, DBDC
3
, góc giữa hai mặt phẳng (ABC) và (DBC) bằng 45 độ. Gọi H là hình chiếu vuông góc của A trên mặt phẳng (DBC) sao cho H và D nằm về hai phía của BC. Tính diện tích S của mặt cầu ngoại tiếp tứ diện ABCD A.
5
π
B.
5
π
4
C.
S
5
π...
Đọc tiếp
Cho tứ diện ABCD có AB=AC= 2 , DB=DC= 3 , góc giữa hai mặt phẳng (ABC) và (DBC) bằng 45 độ. Gọi H là hình chiếu vuông góc của A trên mặt phẳng (DBC) sao cho H và D nằm về hai phía của BC. Tính diện tích S của mặt cầu ngoại tiếp tứ diện ABCD
A. 5 π
B. 5 π 4
C. S = 5 π 8
D. S = 5 π 16
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng
P
:
x
+
y
-
z
+
2
0
và hai điểm
A
7
;
-
4
;
-
3
,
B
3
;
4
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz,cho mặt phẳng P : x + y - z + 2 = 0 và hai điểm A 7 ; - 4 ; - 3 , B 3 ; 4 ; 1 . Gọi M a ; b ; c là điểm thuộc P a < 2 sao cho tam giác AMB vuông tại M và có diện tích nhỏ nhất. Giá trị của biểu thức 3 a + 9 b + 63 c bằng
A. 140
B. -38
C. 154
D. -21
1. Cho hàm số y2x-1/x-1 . Lấy M thuộc C với XMm . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M 2.cho yx+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau 3. cho y x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5) 4 . cho y x+1/x-1 . CMR (d) : 2x-y+m0 luôn cắt C tại A,B trên 2 nhánh củ...
Đọc tiếp
1. Cho hàm số y=2x-1/x-1 . Lấy M thuộc C với XM=m . tiếp tuyến của C tại M cắt 2 đường tiệm cận tại A,B . Gọi I là giao của 2 đường tiệm cận . CMR : M là trung điểm của AB và tam giác IAB có diện tích không phụ thuộc vào M
2.cho y=x+2/x-3 tìm M thuộc C sao cho khoảng cách từ M đến 2 đường tiệm cận C bằng nhau
3. cho y = x+2/x-2 tìm M thuộc C sao cho M cách đều hai trục tọa độ . viết pttt của C biết tiếp tuyến đó đi qua A(-6;5)
4 . cho y = x+1/x-1 . CMR (d) : 2x-y+m=0 luôn cắt C tại A,B trên 2 nhánh của (C) . tìm m để AB ngắn nhất
Cho phần vật thể A giới hạn bởi hai mặt phẳng
x
0
;
x
1
cắt phần vật thể B bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
0
≤
x
≤
1
ta được thiết diện là một tam giác đều có độ dài canh bằng
x
1
−
x
.
Tính thể t...
Đọc tiếp
Cho phần vật thể A giới hạn bởi hai mặt phẳng x = 0 ; x = 1 cắt phần vật thể B bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 1 ta được thiết diện là một tam giác đều có độ dài canh bằng x 1 − x . Tính thể tích phần vật thể B.
A. 3 4
B. 3 48
C. 3 6
D. 3 12
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi
V
1
;
V
2
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính
V
1
+
V
2
A.
17
2...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi V 1 ; V 2 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính V 1 + V 2
A. 17 2 216
B. 17 2 72
C. 17 2 144
D. 2 12