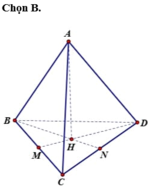
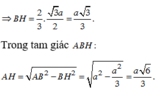
Gọi hình chiếu vuông góc hạ từ A đến mặt phẳng (BCD) là H. Khoảng cách từ A đến mặt phẳng (BCD) là AH.
Vì tứ diện đều nên H là trọng tâm tam giác BCD
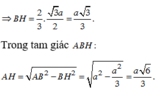
Cho tứ diện đều ABCD. Biết khoảng cách từ A đến mặt phẳng (BCD) bằng 6. Tính thể tích V tứ diện đều ABCD.
A. V = 5 3
B. V = 27 3
C. V = 27 3 2
D. V = 9 3 2
Cho tứ diện đều ABCD. Biết khoảng cách từ điểm A đến mặt phẳng (BCD) bằng 6. Tính thể tích của tứ diện ABCD
A. V = 27 3
B. V = 5 3
C. V = 27 3 2
D. V = 9 3 2
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC),AC =AD = 4, AB =3, BC = 5. Tính khoảng cách d từ điểm A đến mặt phẳng (BCD).
A. d = 12 34
B. d = 60 769
C. d = 769 60
D. d = 34 12
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng A B C , A C = A D = 4 , A B = 3 , B C = 5. Tính khoảng cách d từ điểm A đến mặt phẳng (BCD)
A. d = 12 34
B. d = 60 769
C. d = 769 60
D. d = 34 12
Cho tứ diện ABCD có đáy BCD 1à tam giác đều cạnh a và có thể tích V = a 3 3 2 . Khoảng cách từ A đến mặt phẳng (BCD) là.
A. a
B. 6a
C. 3a
D. 2a
Cho tứ diện đều ABCD có cạnh bằng a Tính khoảng cách từ đỉnh B đến mặt phẳng (ACD)
A. a 6 2
B. a 3 2
C. a 6 3
D. a 2 3
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC = AD = 4, AB = 3, BC = 5. Tính khoảng cách từ điểm A đến mặt phẳng (BCD).
A. 34 12
B. 12 34
C. 769 60
D. 60 769
Cho tứ diện ABCD có BCD tam giác đều cạnh a, A B ⊥ B C D vàAB=a. Tính khoảng cách từ điểm D đến (ABC)?
A. a 3 4
B. a 3 2
C. a 2
D. a 3
Cho tứ diện ABCD có A B = a , A C = 2 , A D = 3 , B A C ^ = C A D ^ = D A B ^ = 90 ° . Khoảng cách từ A đến mặt phẳng (BCD) là
A. 6 7
B. 6 13 13
C. 2 5 5
D. 6 10 10
