Đáp án D
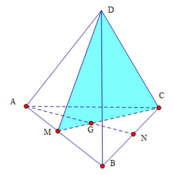
Thiết diện là tam giác cân MCD trong đó M là trung điểm AB n
Ta có D M = C M = a 3 2 ; C D = a
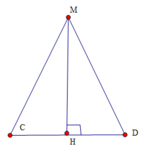
Gọi H là trung điểm
C D ⇒ M H = M C 2 − C H 2 = 3 a 2 4 − a 2 4 = a 2 2
S M C D = 1 2 M H . C D = 1 2 a 2 2 . a = a 2 2 4
Đáp án D


Thiết diện là tam giác cân MCD trong đó M là trung điểm AB n
Ta có D M = C M = a 3 2 ; C D = a
Gọi H là trung điểm
C D ⇒ M H = M C 2 − C H 2 = 3 a 2 4 − a 2 4 = a 2 2
S M C D = 1 2 M H . C D = 1 2 a 2 2 . a = a 2 2 4
Cho tứ diện đều ABCD cạnh a. Gọi M,N,G lần lượt là trung điểm của các cạnh AB, BC và trọng tâm tam giác ACD. Diện tích của thiết diện khi cắt tứ diện bởi mặt phẳng (MNG) bằng
A. 7 a 2 3 48
B. 7 a 2 3 24
C. a 2 3 16
D. a 2 3 48
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác BCD. Gọi S là điểm đối xứng của G mặt phẳng (ABC). Thể tích khối đa diện SABCD là:
A. a 3 2
B. a 3 2 3
C. a 3 2 6
D. a 3 2 9
Cho tứ diện đều ABCD có độ dài các cạnh bằng 2a . Gọi M , N lần lượt là trung điểm các cạnh AC , BC ; P là trọng tâm tam giác BCD . Mặt phẳng (MNP) cắt tứ diện theo một thiết diện có diện tích là:
A. a 2 11 2
B. a 2 2 4
C. a 2 11 4
D. a 2 3 4
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
A. S = a 2 2
B. S = a 2 3 6
C. S = a 2 3 9
D. S = a 2 6
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C, D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T).
A. S = a 2 2 .
B. S = a 2 3 6 .
C. S = a 2 3 9 .
D. S = a 2 6 .
Cho tứ diện đều ABCD có các cạnh bằng a. Gọi M là trung điểm của cạnh BC. Tính diện tích thiết diện của tứ diện khi cắt bởi mặt phẳng đi qua M và song song với mặt phẳng (ABD)
A. a 2 3 4
B. a 2 3 8
C. a 2 3 16
D. a 2 3 12
Cho hình chóp tứ giác đều S.ABCD, đuờng cao SO. Biết rằng trong các thiết diện của hình chóp cắt bởi các mặt phẳng chứa SO, thiết diện có diện tích lớn nhất là tam giác đều cạnh bằng a, tính thể tích khối chóp đã cho
A. a 3 2 6
B. a 3 3 12
C. a 3 3 4
D. a 3 3 6
Trong không gian Oxyz. Cho tứ diện đều ABCD có A(0;1;2) và hình chiếu vuông góc của A trên mặt phẳng (BCD) là H (4; -3;-2). Tọa độ tâm I của mặt cầu ngoại tiếp tứ diện ABCD.
A. I(3; -2;-1).
B. I(2;-1;0).
C. I(3; -2;1).
D. I(-3; -2;1).
Cho tứ diện ABCD có A B = A C = 2 , B C = 2 , D B = D C = 3 , góc giữa hai mặt phẳng A B C và D B C bằng 45 ° . Gọi H là hình chiếu vuông góc của A trên mặt phẳng D B C sao cho H và D nằm về hai phía của BC. Tính diện tích S của mặt cầu ngoại tiếp tứ giác ABCD.
A. S = 5 π
B. S = 5 π 4
C. S = 5 π 8
D. S = 5 π 16