Các câu hỏi tương tự
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. M thuộc đoạn thẳng BC sao cho BM = 2MC. Giao tuyến của mặt phẳng (BGM) và (ACD)
Cho tứ diện ABCD ; gọi G là trọng tâm tam giác BCD và M là trung điểm CD; I là điểm ở trên đoạn thẳng AG; BI cắt (ACD) tại J. Chọn khẳng định sai?
A. giao tuyến của (ACD) và ( ABG) là AM
B. 3 điểm A; J; M thẳng hàng
C. J là trung điểm của AM
D. giao tuyến của (ACD) và ( BDJ) là DJ
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là: A. B. C. D.
Đọc tiếp
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:
A. ![]()
B. ![]()
C. ![]()
D. 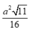
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD. A.
a
2
3
4
B.
a
2
3
9
C. ...
Đọc tiếp
Cho tứ diện ABCD cạnh a. Gọi G là trọng tâm của tam giác ABC. Qua G dựng một mặt phẳng (P) song song với mặt phẳng (P) song song với mặt phẳng (BCD). Tìm diện tích thiết diện của (P) và tứ diện ABCD.
A. a 2 3 4
B. a 2 3 9
C. a 2 2 16
D. a 2 3 18
Cho tứ diện ABCD và điểm G thỏa mãn
G
A
⇀
+
G
B
⇀
+
G
C
⇀
+
G
D
⇀
0
⇀
(G gọi là tr...
Đọc tiếp
Cho tứ diện ABCD và điểm G thỏa mãn G A ⇀ + G B ⇀ + G C ⇀ + G D ⇀ = 0 ⇀ (G gọi là trọng tâm của tứ diện). Gọi G A = G A ∩ ( B C D ) . Trong các khẳng định sau, khẳng định nào đúng?
A. G A ⇀ = - 3 G A G ⇀
B. G A ⇀ = 4 G A G ⇀
C. G A ⇀ = 3 G A G ⇀
D. G A ⇀ = 2 G A G ⇀
Cho tứ diện ABCD. Gọi G và E lần lượt là trọng tâm của tam giác ABD và ABC. Mệnh đề nào dưới đây đúng:
A. GE//CD
B. GE và CD chéo nhau
C. GE cắt AD
D. GE cắt CD
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC; G là trọng tâm
∆
BCD. Khi đó giao điểm của đường thẳng MG và mp(ABC) là: A. điểm C B. điểm N C. giao điểm của đường thẳng MG và đường thẳng AN D. giao điểm của đường thẳng MG và đường thẳng BC
Đọc tiếp
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC; G là trọng tâm ∆ BCD. Khi đó giao điểm của đường thẳng MG và mp(ABC) là:
A. điểm C
B. điểm N
C. giao điểm của đường thẳng MG và đường thẳng AN
D. giao điểm của đường thẳng MG và đường thẳng BC
Cho tứ diện ABCD có E và F lần lượt là trung điểm của AB và CD; G là trọng tâm tam giác BCD. Giao điểm của đường thẳng EG và mp (ACD) là
A. điểm F
B. giao điểm của EG và AF
C. Giao điểm của EG và AC
D. giao điểm của EG và CD
Cho tứ diện ABCD có G là trọng tâm tam giác ABC. Gọi M là trung điểm AB P, là điểm nằm trên đoạn AD sao cho MP không song song BD. Giao tuyến của ( ) MPG và ( ) BCD là







