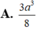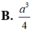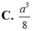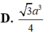Gọi M là trung điểm AB
\(\Rightarrow\left\{{}\begin{matrix}CM\perp AB\\DM\perp AB\end{matrix}\right.\) (trong tam giác đều trung tuyến đồng thời là đường cao)
\(\Rightarrow AB\perp\left(CDM\right)\)
\(\Rightarrow AB\perp CD\)
Gọi M là trung điểm AB
\(\Rightarrow\left\{{}\begin{matrix}CM\perp AB\\DM\perp AB\end{matrix}\right.\) (trong tam giác đều trung tuyến đồng thời là đường cao)
\(\Rightarrow AB\perp\left(CDM\right)\)
\(\Rightarrow AB\perp CD\)
Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Góc giữa AB và CD là?
Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Góc giữa AB và CD là?
A.120°
B. 60°
C. 90°
D. 30°
Cho tứ diện ABCD có hai mặt ABC và ADC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác ABC vuông tại A có AB =a, AC =b. Tam giác ACD vuông tại D có CD = a.
a) Chứng minh các tam giác BAD và BDC là các tam giác vuông.
b) Gọi I và K lần lượt là trung điểm của AD và BC. Chứng minh IK là đường vuông góc chung của hai đường thẳng AD và BC.
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (BCD). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh (ABC)⊥(DFK)
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (BCD). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh (ABE)⊥(ADC)
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (BCD). Gọi BE và DF là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Chứng minh (DFK)⊥(ACD)
Cho tứ diện ABCD có các mặt ABC, ABD là các tam giác vuông. Gọi M ,N lần lượt là hình chiếu vuông góc của B trên CD, AM.
Chứng minh rằng:
AB \(\perp\)(BCD)
BN \(\perp\) (ABM)
Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung đáy BC. Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng BC vuông góc với mặt phẳng (ADI)
b) Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc với mặt phẳng (BCD).
Cho tứ diện ABCD có hai mặt ABC, BCD là các tam giác đều cạnh a và nằm trong các mặt phẳng vuông góc với nhau. Thể tích của khối tứ diện ABCD là: