Question

 Cho tứ diện ABCD có G là trọng tâm ABC  và M thuộc cạnh AD sao cho AD=3MD.               

a). Chứng minh MG//(BCD).                                                         b). Tìm giao điểm của DG và (MBC). 

Answer 1

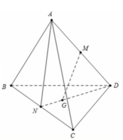
a) Gọi N là trung điểm BC

Xét ΔAND có: 

`(AG)/(AN) = (AM)/(AD) = 2/3` (Do G là trong tâm ΔABC)

`=> GM` //` ND` (Talet đảo)

mà `ND ⊂ (BCD)`

`=> GM` // `(BCD)`

 

Answer 2

b) `M ∈ AD ⊂ (AND); M  ⊂ (MBC)`

`N ⊂ (AND); N ∈ BC ⊂ (MBC)`

`=> (MBC)` \(\cap\) `(AND) = MN`

`=> MN ⊂ (AND) `

Gọi `L = MN` \(\cap\) `GD`

`=> L = (BCM) ` \(\cap\) `GD`